Skip over navigation
This printable worksheet may be useful: Guttter.
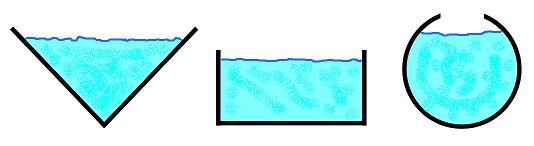
Some learners may access this general problem more successfully if a particular cross-section (profile) type is specified at the start: a simple rectangle for example. This could lead into consideration of a trapezium (removing the constraint of vertical sides) .
Algebra could feature at several points in this problem. For example when learners are :
Gutter
Age 14 to 16
Challenge Level 
This printable worksheet may be useful: Guttter.
Some learners may access this general problem more successfully if a particular cross-section (profile) type is specified at the start: a simple rectangle for example. This could lead into consideration of a trapezium (removing the constraint of vertical sides) .
Algebra could feature at several points in this problem. For example when learners are :
- identifying useful variables;
- working with a simple rectanglular profile,several depth values might be used,producing different profile areas which could be plotted;
- utilising a spreadsheet, deriving a general formula for calculating the profile area based on depth.
Interpretation of the calculated results is needed and involves considering the proportions between lengths and and the implications of that for the shape of the profile.
There is an interesting general principle underlying this problem: that if the profile is based on a regular polygon the optimum cross-section is half of that polygon.
Unrushed discussion of why this is the case might lead to connections being made with other optimisation problems related to area or volume.
Familiarity with mathematics may lead us instinctively towards a circular profile as the optimum solution (i.e. a pipe). But that is not in fact anywhere near the best form, and the experience of challenging this misconception can be a pathway into new understanding.
You may also like
The Fastest Cyclist
Andy is desperate to reach John o'Groats first. Can you devise a winning race plan?