Cuboid Challenge

Cuboid Challenge printable sheet

Take a square sheet of paper 20cm by 20cm, cut identical squares from each corner, and fold up the flaps to make a box (without a lid).

  

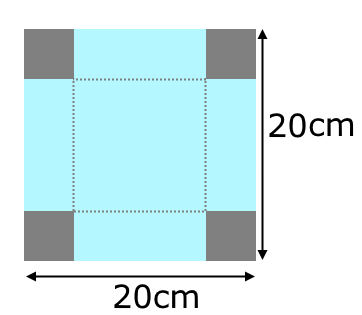
What is the volume of your box?
What different volumes can you make by varying the size of the squares you cut out?

What is the maximum possible volume of this type of box that can be made from a 20cm by 20cm square of paper?

Now try starting with different sized square sheets of paper.

Can you find a relationship between the size of paper and the size of the square cut-out that produces the maximum volume?



Click here for a poster of this problem.