Skip over navigation
Siddhant from Singapore International School in India, Astrid, Anaira and Millie from CLSG in the UK and Ethan, Amaya and Lily from Pangkok Patana School in Thailand tested different cut sizes. This is Astrid, Anaira and Millie's work:

Ethan, Amaya and Lily used a spreadsheet to show that 3.333 was the best option with 3 decimal places. Click here to see their spreadsheet.
Arya from West Island School in Hong Kong got to the same answer using spatial reasoning:
I think the identical square to be cut from each corner has a length of 3.33 recurring cm.
Method
Every time you increase the height by 1 the length reduces by 2 each side.
Normally a cube will have a bigger volume than a cuboid that has lets say 2 cm more of height and 2 cm less than the original length.
But this time the ratio is 1:2 (because increasing the height by 1 cm decreases the length by 2 cm).
So the [ratio of] height to length is 1:2.
So 13.33333 and 6.66666
6.6666 has to be divided by two because it is minused from both sides.
Ethan, Amaya and Lily also tried starting from a 15 cm by 15 cm sheet of paper:
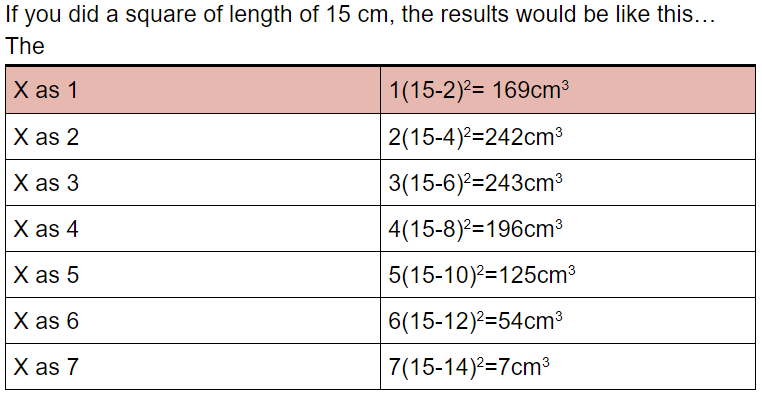
Year 9 Set 1 from British International School Phuket in Thailand tried a variety of different sizes. This is their work:
We used Desmos to plot the graphs and find the maximum volume.
Investigation 1
Conclusions: For an $n$ by $n$ square the value of $x$ that maximizes the volume is given by $\frac n6$
Investigation 2
Conclusions: For a $10$ by $n$ square the value of $x$ that maximizes the volume approaches $2.5$ as $n$ gets large (approaches infinity).
Investigation 3
Conclusions: For an $m$ by $n$ square the value of $x$ that maximizes the volume approaches $\frac m 4$ as $n$ gets large (approaches infinity).
Hyochan from Brighton College Abu Dhabi in UAE and Scott, Jakob, Max and Timmy from Abingdon School in the UK used a different approach for the 20 by 20 sheet of paper. This is Hyochan's work:
Since the problem is about finding the maximum volume of a cuboid, I thought about using differentiation.
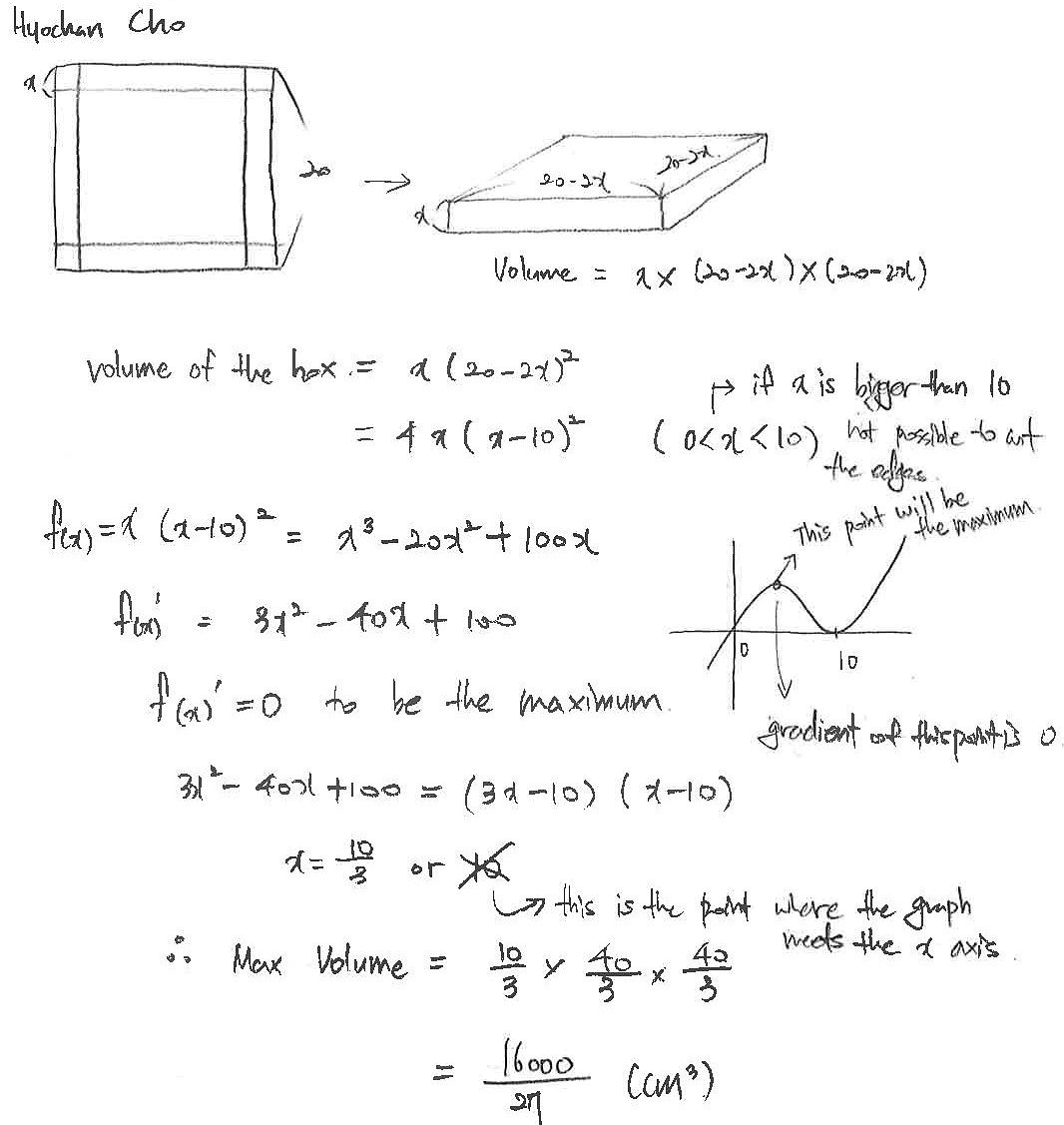
Max referred back to the original problem to explain why $x=10$ couldn't be a maximum:
I put $10$ back into the original cubic and it gave me the answer $0.$ This is because when $x=10$ there is no paper as $10\times2=20.$
Scott, Jakob and Timmy used more calculus to check that $x=\frac{10}3$ is a maximum. This is Jakob's work:
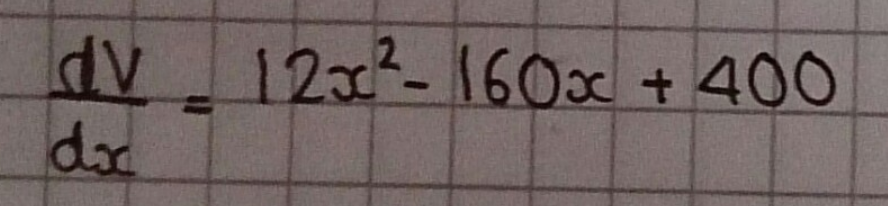
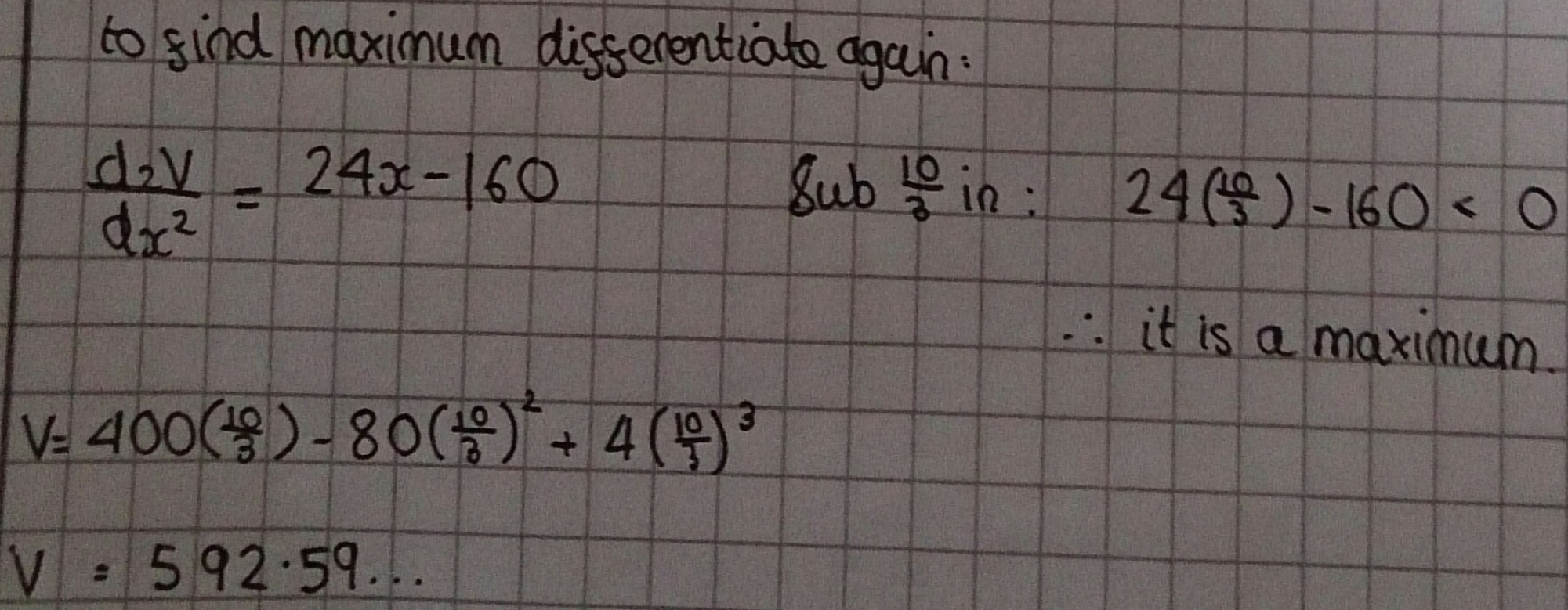
Max applied this method to differently sized sheets of paper:
I did this method again with $40$ cm of paper which gave me an $x$ of $\frac{20}3$ and volume of $4740.740$ recurring. I also did it with $65$ cm and got an $x$ of $\frac{65}{6}$ and volume of $20342.592$ recurring. From this the pattern for the maximum $x$ is the full edge of the paper divided by $6$.
I also found that the volume pattern is the previous volume times the multiplier of the edge cubed. For example, the volume of the $40$ cm piece of paper is $592.592$ (volume of $20 $cm piece) times $2^3=8$ which is $4740.740.$ The volume of the $65$ cm piece is $4740.740$ times $\frac{65}{40}=1.625$ cubed ($4.29$ (3sf)) which is $20342.592.$
Timmy and Charlie from Abingdon School and Ana from Bangkok Patana School generalised this. Ana wrote:
From this I can calculate that the formula for a box's volume constructed from a square with any length ($l$) is $$volume=(l-2x)^2\left(x\right)=l^2x-4lx^2+4x^3$$
Additionally the $x$ value which gives the largest volume is $\frac{\text{length of square}}{6}$
The maximum value is the maximum stationary point of the graph which can be found using differentiation. $$\frac{\text{d}}{\text{d}x}\left(4x^3-4lx^2+l^2x\right)=12x^2-8lx+l^2$$
The maximum point's derivative must equal $0$, thus at the maximum $12x^2-8lx+l^2=0.$
By using the quadratic equation, the root values can be found. $$\frac{8l\pm\sqrt{64l^2-48l^2}}{24}=\frac{8l\pm\sqrt{16l^2}}{24}=\frac{8l\pm4l}{24}$$
The maximum value cannot exceed half of the length of the square, thus the stationary point calculated is the smaller value. So the maximum point is at the $x$ value $$\frac{4l}{24}=\frac{l}{6}$$
Charlie checked that this is a maximum (not minimum) value by differentiating again (Charlie and Timmy use $y$ instead of $l$ for the side length of the sheet of paper):
At maximum $\dfrac{\text{d}^2V}{\text{d}x^2}<0$
$\dfrac{\text{d}^2V}{\text{d}x^2}=24x-8y$
$24\left(\frac y 6 \right)- 8y = -4y$ - this is the maximum
$24\left(\frac y2\right)-8y= 4y$
Charlie, Ana and Timmy found the maximum volume and checked that this agrees with the values found for the 20 by 20 sheet of paper. This is Timmy's work:


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cuboid Challenge
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Siddhant from Singapore International School in India, Astrid, Anaira and Millie from CLSG in the UK and Ethan, Amaya and Lily from Pangkok Patana School in Thailand tested different cut sizes. This is Astrid, Anaira and Millie's work:

Ethan, Amaya and Lily used a spreadsheet to show that 3.333 was the best option with 3 decimal places. Click here to see their spreadsheet.
Arya from West Island School in Hong Kong got to the same answer using spatial reasoning:
I think the identical square to be cut from each corner has a length of 3.33 recurring cm.
Method
Every time you increase the height by 1 the length reduces by 2 each side.
Normally a cube will have a bigger volume than a cuboid that has lets say 2 cm more of height and 2 cm less than the original length.
But this time the ratio is 1:2 (because increasing the height by 1 cm decreases the length by 2 cm).
So the [ratio of] height to length is 1:2.
So 13.33333 and 6.66666
6.6666 has to be divided by two because it is minused from both sides.
Ethan, Amaya and Lily also tried starting from a 15 cm by 15 cm sheet of paper:
Year 9 Set 1 from British International School Phuket in Thailand tried a variety of different sizes. This is their work:
We used Desmos to plot the graphs and find the maximum volume.
Investigation 1
| Square size | Equation for Volume ($V$) |
Value of $x$ that maximizes $V$ |
|---|---|---|
| $10 \times 10$ | $(10-2x)(10-2x)x$ | $\frac53$ |
| $20 \times 20$ | $(20-2x)(20-2x)x$ | $\frac{10}3$ |
| $30 \times 30$ | $(30-2x)(30-2x)x$ | $5$ |
| $40 \times 40$ | $(40-2x)(40-2x)x$ | $\frac{20}{3}$ |
| $50 \times 50$ | $(50-2x)(50-2x)x$ | $\frac{25}{3}$ |
| $n\times n$ | $(n - 2x)(n - 2x)x$ | $\frac n6$ |
Conclusions: For an $n$ by $n$ square the value of $x$ that maximizes the volume is given by $\frac n6$
Investigation 2
| Paper size | Equation for
Volume ($V$)
|
Value of $x$ that maximizes $V$ |
|---|---|---|
| $10 \times 10$ | $(10-2x)(10-2x)x$ | $\frac53=1.667$ |
| $10 \times 20$ | $(10-2x)(20-2x)x$ | $2.113$ |
| $10 \times 30$ | $(10-2x)(30-2x)x$ | $2.257$ |
| $10 \times 40$ | $(10-2x)(40-2x)x$ | $2.324$ |
| $10 \times 50$ | $(10-2x)(50-2x)x$ | $2.362$ |
| $10 \times 1000$ | $ (10-2x)(1000-2x)x$ | $2.494$ |
| $10 \times 10000$ | $(10-2x)(10000-2x)x$ | $2.499$ |
Conclusions: For a $10$ by $n$ square the value of $x$ that maximizes the volume approaches $2.5$ as $n$ gets large (approaches infinity).
Investigation 3
| Paper size | Value that $x$ approaches as $n$ approaches infinity |
|---|---|
| $10 \times n$ | $2.5$ |
| $1=20 \times n$ | $5$ |
| $30 \times n$ | $7.5$ |
| $40 \times n$ | $10$ |
| $m\times n$ | $\frac m 4$ |
Conclusions: For an $m$ by $n$ square the value of $x$ that maximizes the volume approaches $\frac m 4$ as $n$ gets large (approaches infinity).
Hyochan from Brighton College Abu Dhabi in UAE and Scott, Jakob, Max and Timmy from Abingdon School in the UK used a different approach for the 20 by 20 sheet of paper. This is Hyochan's work:
Since the problem is about finding the maximum volume of a cuboid, I thought about using differentiation.

Max referred back to the original problem to explain why $x=10$ couldn't be a maximum:
I put $10$ back into the original cubic and it gave me the answer $0.$ This is because when $x=10$ there is no paper as $10\times2=20.$
Scott, Jakob and Timmy used more calculus to check that $x=\frac{10}3$ is a maximum. This is Jakob's work:
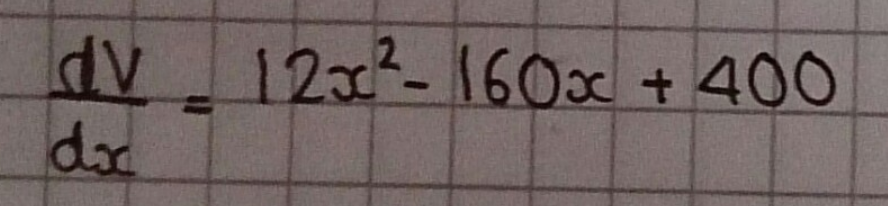
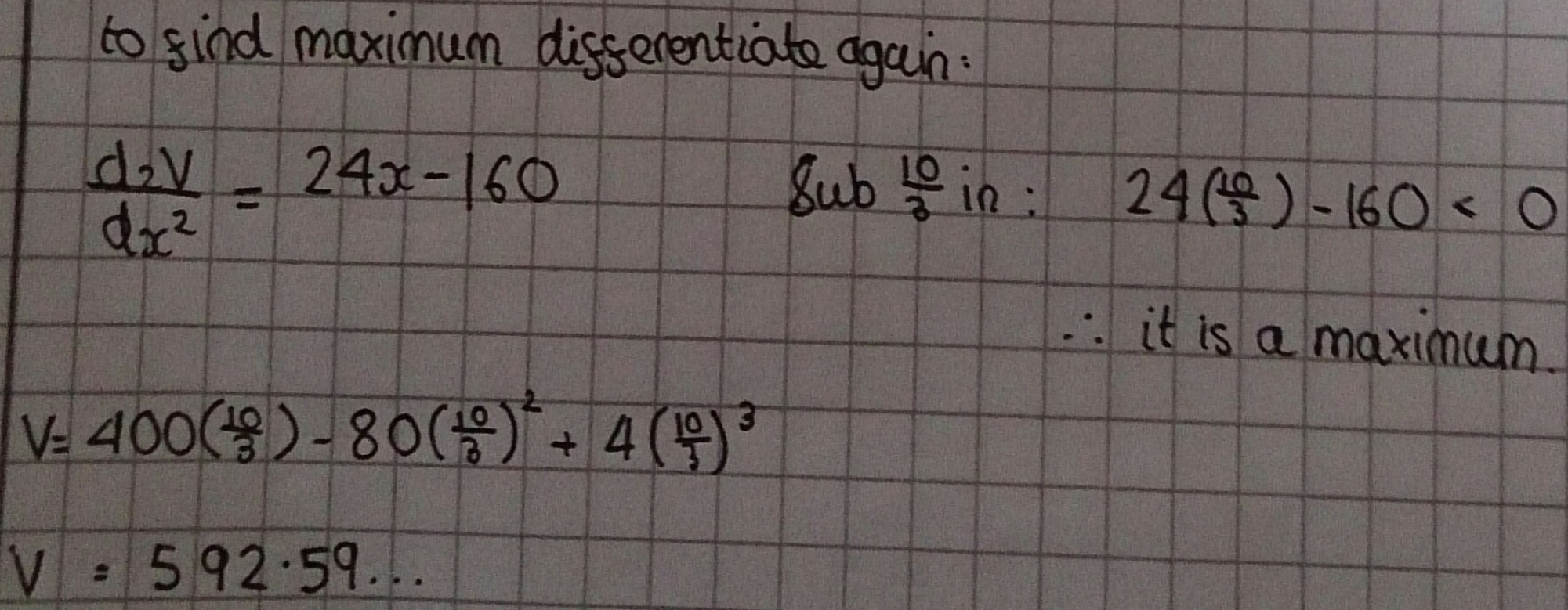
Max applied this method to differently sized sheets of paper:
I did this method again with $40$ cm of paper which gave me an $x$ of $\frac{20}3$ and volume of $4740.740$ recurring. I also did it with $65$ cm and got an $x$ of $\frac{65}{6}$ and volume of $20342.592$ recurring. From this the pattern for the maximum $x$ is the full edge of the paper divided by $6$.
I also found that the volume pattern is the previous volume times the multiplier of the edge cubed. For example, the volume of the $40$ cm piece of paper is $592.592$ (volume of $20 $cm piece) times $2^3=8$ which is $4740.740.$ The volume of the $65$ cm piece is $4740.740$ times $\frac{65}{40}=1.625$ cubed ($4.29$ (3sf)) which is $20342.592.$
Timmy and Charlie from Abingdon School and Ana from Bangkok Patana School generalised this. Ana wrote:
From this I can calculate that the formula for a box's volume constructed from a square with any length ($l$) is $$volume=(l-2x)^2\left(x\right)=l^2x-4lx^2+4x^3$$
Additionally the $x$ value which gives the largest volume is $\frac{\text{length of square}}{6}$
The maximum value is the maximum stationary point of the graph which can be found using differentiation. $$\frac{\text{d}}{\text{d}x}\left(4x^3-4lx^2+l^2x\right)=12x^2-8lx+l^2$$
The maximum point's derivative must equal $0$, thus at the maximum $12x^2-8lx+l^2=0.$
By using the quadratic equation, the root values can be found. $$\frac{8l\pm\sqrt{64l^2-48l^2}}{24}=\frac{8l\pm\sqrt{16l^2}}{24}=\frac{8l\pm4l}{24}$$
The maximum value cannot exceed half of the length of the square, thus the stationary point calculated is the smaller value. So the maximum point is at the $x$ value $$\frac{4l}{24}=\frac{l}{6}$$
Charlie checked that this is a maximum (not minimum) value by differentiating again (Charlie and Timmy use $y$ instead of $l$ for the side length of the sheet of paper):
At maximum $\dfrac{\text{d}^2V}{\text{d}x^2}<0$
$\dfrac{\text{d}^2V}{\text{d}x^2}=24x-8y$
$24\left(\frac y 6 \right)- 8y = -4y$ - this is the maximum
$24\left(\frac y2\right)-8y= 4y$
Charlie, Ana and Timmy found the maximum volume and checked that this agrees with the values found for the 20 by 20 sheet of paper. This is Timmy's work:

You may also like
Plutarch's Boxes
According to Plutarch, the Greeks found all the rectangles with integer sides, whose areas are equal to their perimeters. Can you find them? What rectangular boxes, with integer sides, have their surface areas equal to their volumes?

