Two Right Angles
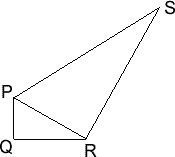
In the figure above, $PQ=2\frac{1}{3}$, $PS = 6\frac{6}{7}$, $PQR$ and $PRS$ are right-angled triangles, and the angles $QPR$ and $RPS$ are the same.
How long is $PR$?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?