Skip over navigation
This article will introduce you to a way of naming knots - you'll need some paper and something to write with so you can try things out as you read ...
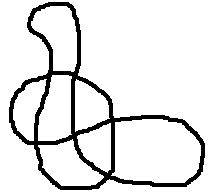
Try drawing a knot with $14$ crossings (a line which crosses itself in $14$ places).
Can you draw a knot with any number of crossings you like?
Now try adding some more information to the knot by showing which string is on top at each crossing. You can do that by drawing the knot again, but with a small gap in the "underneath" line when part of the rope goes under another part, like this:
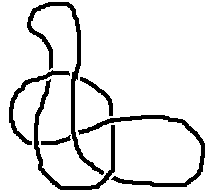
Can you choose which way the crossings go so that the string would unravel into an untangled loop?
If you draw the string so that as you follow it round it goes alternately under then over then under then over at crossings, you have drawn an alternating knot. Have a go: as you follow the string round, do you find that when you get to a crossing where you've already been, it's already the right way round? And when you get back to the beginning, does the sequence continue (if you started with an "over" do you end with an "under")?
Can you prove that this always works?
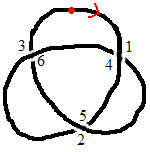
I could write the pairs of numbers for the crossings out like this:
So, now you know that even knots can be named mathematically. You might also be interested to know that the symmetries of knots can be used to distinguish some from others, and in addition can help to determine whether a knot is invertible. If you're keen to try this for yourself, have a go at The Invertible Trefoil .
For a different, but related, challenge you might like to look at the problems Twisting and Turning and More Twisting and Turning which introduce you to the idea of tangles.
Drawing Doodles and Naming Knots
This article will introduce you to a way of naming knots - you'll need some paper and something to write with so you can try things out as you read ...
Taking a Line for a Walk
You can start thinking about knots by drawing them as lines. To draw a knot, you just need to draw a closed loop which crosses over itself, like the one in the picture. Don't worry about which string goes on top and which goes underneath for the moment.Try drawing a knot with $14$ crossings (a line which crosses itself in $14$ places).
Can you draw a knot with any number of crossings you like?
Now try adding some more information to the knot by showing which string is on top at each crossing. You can do that by drawing the knot again, but with a small gap in the "underneath" line when part of the rope goes under another part, like this:
Can you choose which way the crossings go so that the string would unravel into an untangled loop?
If you draw the string so that as you follow it round it goes alternately under then over then under then over at crossings, you have drawn an alternating knot. Have a go: as you follow the string round, do you find that when you get to a crossing where you've already been, it's already the right way round? And when you get back to the beginning, does the sequence continue (if you started with an "over" do you end with an "under")?
Can you prove that this always works?
Naming Knots
Draw yourself a new knot, choosing which way the strands go at
each crossing however you like.
Mark a starting point somewhere on the string and an arrow
pointing in one direction or the other along the string. Now follow
the string round your knot from the starting point in the direction
of the arrow. The first time you come to a crossing, label it $1$.
The next time you come to a crossing, label it $2$, and so on. By
the time you get back to your starting point, each crossing should
have $2$ labels.
What do you notice about the pairs of labels? Can you explain
the observation?
Here is a knot labelled the way I have described. (The red dot
and arrow are the starting point and direction).
I could write the pairs of numbers for the crossings out like this:
| 1 | 3 | 5 |
| 4 | 6 | 2 |
The top line is the odd number, arranged in order. The bottom
line shows which even number is at the same crossing as each odd
number.
Try writing the numbers on your knot out like this.
Now see if you can draw a knot which would have these numbers:
(the numbers don't tell you which strand is on top at a crossing,
so you can't draw the "unders" and "overs").
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 12 | 14 | 10 | 2 | 4 | 16 | 8 | 6 |
In fact, we know what the top line of numbers is going to be -
it's just the odd numbers $1,\ 3,\ 5\ldots$. So we could miss it
out altogether. The line which is left is a kind of name for the
knot.
Can you draw a knot whose "name" is $4 \; 8 \; 6 \; 2$? It
might help to write out the two-line table (with the odd numbers
too) first.
Now try $8 \; 6 \; 2 \; 4$. And then $6 \; 2 \; 4 \; 8$. What
do you notice about these three sets of numbers, and the knots they
represent?
What about $4 \; 6 \; 8 \; 2$?
In Conclusion
So, now you know that even knots can be named mathematically. You might also be interested to know that the symmetries of knots can be used to distinguish some from others, and in addition can help to determine whether a knot is invertible. If you're keen to try this for yourself, have a go at The Invertible Trefoil .
For a different, but related, challenge you might like to look at the problems Twisting and Turning and More Twisting and Turning which introduce you to the idea of tangles.
Related Collections
You may also like
Ball Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?
Cushion Ball
The shortest path between any two points on a snooker table is the straight line between them but what if the ball must bounce off one wall, or 2 walls, or 3 walls?