Difference Sudoku

If you can manage to reduce the possibilities of one cell to 2 or 3 numbers, you could try solving the puzzle with each of those values in turn. If  you reach a contradiction (for example a number is repeated in a row, column or square) then you can rule out that value and try one of the others instead.

Here's an example of a way to start this puzzle. Let's look at this section of the grid:

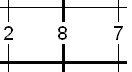
We need two numbers that differ by 8, they can only be 1 and 9.
But which way round  should they go?
Let's try both possibilities, writing one pair at the top of the cells and the other at the bottom:

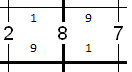
Then we can use the '7' to determine the value of the next cell for each of our possibilities:

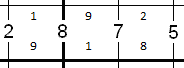
We can keep going in this way with two possible solutions emerging until one of them ends in a contradiction.

Rosie and Zoe solved this Sudoku. They kept a record of the order in which they filled the Sudoku and wrote it in the boxes. Their journey can be found here. This is just one possible route through the problem.