Skip over navigation
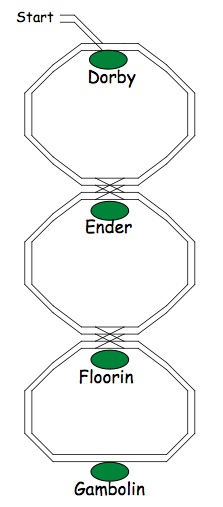
Well, here's a train route. The train starts at the top and makes a number of visits to the stations.
Now let's suppose that the train is going to make visits to three stations (they do not have to be different stations - each station can be visited several times!).
Simple Train Journeys
Age 5 to 11
Challenge Level 
Well, here's a train route. The train starts at the top and makes a number of visits to the stations.
Now let's suppose that the train is going to make visits to three stations (they do not have to be different stations - each station can be visited several times!).
So the first station would be Dorby
- this will always be the case! (Why?)
Then the train can go on to Ender.
When at Ender it could return and visit Dorby again OR it could go
on to Floorin.
So two different journeys:
Dorby - Ender - Floorin
Dorby - Ender - Dorby
Your challenge is to find all the different journeys for visiting four stations.
You could then go on to find all the
different journeys for visiting more stations - try five.
How about six stations?
Can you predict the number of different journeys for visiting seven stations? Were you right?
How would you predict the number of
different journeys for visiting eight stations?
You might like to then invent your own routes that may go further than this one and then answer similar questions that you can think up.
You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Doplication
We can arrange dots in a similar way to the 5 on a dice and they usually sit quite well into a rectangular shape. How many altogether in this 3 by 5? What happens for other sizes?