Skip over navigation
Some good thinking from Berny at Gordonstoun School, and others, connecting the algebra to the shape and position of the quadratic graph (parabola) :
When we set a problem on the NRICH site there's often an insight we hope you'll discover as you work your way around the problem.
In Minus One Two Three the insight was to see that expressions a. b. and c. below are just three different ways to represent the same quadratic form.
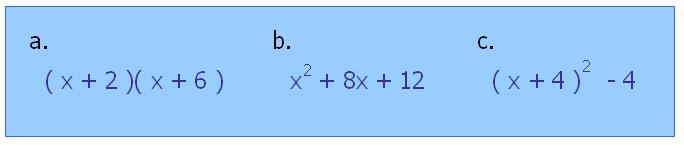
It's, b, the second of those three forms, which helps most here because it reveals the axis of symmetry for the red graph below ( the blue graph is a simple x-squared parabola passing through the origin )
Looking at c. we can see that $x = -4$ will produce the lowest possible value for this expression ( $-4$ ).
The '$+ 4$' in the expression works like a boost for the $x$ value and lets everything on the $x$-squared curve happen $4$ 'earlier' - that is to the left of the origin.
Subtracting $4$, after the 'squaring', has the effect of lowering all values, or points on the graph, by $4$.
So c. is like the $x$-squared parabola but shifted four left and four down.
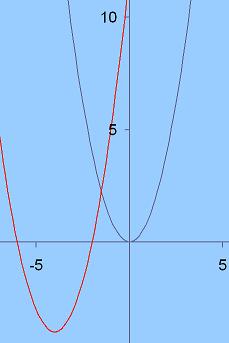
For x smaller than $-4$ the graph will be 'falling' towards this minimum value and to the right (greater than $-4$) the graph will 'climb' again.
So as x values move from $-3$ , to $-2$ , to $-1$ , the value of the expression will be increasing, away to the right of that minimum point of $x = -4$.
So $-3$ will produce the lowest of these three values, and $-1$ will produce the highest.
In a similar way with the other expressions :
$(2x + 7)(x + 1)$ produces middle, lowest, and highest of the three values when $x = -3$, $-2$, and $-1$
$(2x - 3)(x + 5)$ produces highest, lowest, and middle of the three values when $x = -3$, $-2$, and $-1$
$(x - 3)(x - 1)$ produces highest, middle, and lowest of the three values when $x = -3$, $-2$, and $-1$
More generally, you might like to think about whether every pair of linear brackets, like a. would produce a parabola-type ($x$-squared) curve, and similarly whether every expression like b. would have to be symmetric about some $x$ value.
Minus One Two Three
Age 14 to 16
Challenge Level 
Some good thinking from Berny at Gordonstoun School, and others, connecting the algebra to the shape and position of the quadratic graph (parabola) :
When we set a problem on the NRICH site there's often an insight we hope you'll discover as you work your way around the problem.
In Minus One Two Three the insight was to see that expressions a. b. and c. below are just three different ways to represent the same quadratic form.
b. is made from a., multiplying to 'remove the brackets', and
c. is decided by looking at b.
Deciding the c. form is sometimes called 'completing the
square', if you are not yet familiar with that, square $( x + 4 )$
to check that the three representations really do match.
It's, b, the second of those three forms, which helps most here because it reveals the axis of symmetry for the red graph below ( the blue graph is a simple x-squared parabola passing through the origin )
Looking at c. we can see that $x = -4$ will produce the lowest possible value for this expression ( $-4$ ).
The '$+ 4$' in the expression works like a boost for the $x$ value and lets everything on the $x$-squared curve happen $4$ 'earlier' - that is to the left of the origin.
Subtracting $4$, after the 'squaring', has the effect of lowering all values, or points on the graph, by $4$.
So c. is like the $x$-squared parabola but shifted four left and four down.
For x smaller than $-4$ the graph will be 'falling' towards this minimum value and to the right (greater than $-4$) the graph will 'climb' again.
So as x values move from $-3$ , to $-2$ , to $-1$ , the value of the expression will be increasing, away to the right of that minimum point of $x = -4$.
So $-3$ will produce the lowest of these three values, and $-1$ will produce the highest.
In a similar way with the other expressions :
$(2x + 7)(x + 1)$ produces middle, lowest, and highest of the three values when $x = -3$, $-2$, and $-1$
$(2x - 3)(x + 5)$ produces highest, lowest, and middle of the three values when $x = -3$, $-2$, and $-1$
$(x - 3)(x - 1)$ produces highest, middle, and lowest of the three values when $x = -3$, $-2$, and $-1$
More generally, you might like to think about whether every pair of linear brackets, like a. would produce a parabola-type ($x$-squared) curve, and similarly whether every expression like b. would have to be symmetric about some $x$ value.
You may also like
Converse
Clearly if a, b and c are the lengths of the sides of an equilateral triangle then a^2 + b^2 + c^2 = ab + bc + ca. Is the converse true?
Consecutive Squares
The squares of any 8 consecutive numbers can be arranged into two sets of four numbers with the same sum. True of false?
Parabolic Patterns
The illustration shows the graphs of fifteen functions. Two of them have equations y=x^2 and y=-(x-4)^2. Find the equations of all the other graphs.