Skip over navigation
Well done to Daniel from Royston and to Georgina from St. George's School for seeing the answer to the first important question :
'Did that tell you something about yellow and green triangles, about how they relate to each other' ?
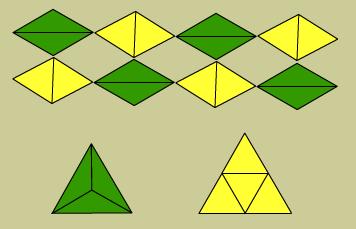
Two yellow triangles make a rhombus of a size which can also be made by two green triangles.
And that lets us see that the yellow and green hexagons are equal because the yellow and green triangles have the same area (half that rhombus) and both hexagons use six triangles. But the equilateral triangles (below) do not use the same number of triangles and so cannot be the same size.
Esther had a great approach using sequences :
You can make equilateral triangle arrangements from yellow triangles :
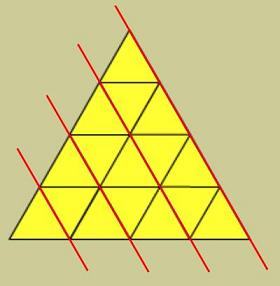
The numbers needed follow the sequence : 1, 4, 9, 16 . . . a ² where a is the number in the sequence.
When I tried making equilateral triangles with the green triangles I could see that one way to do it was by replacing each equilateral space with three green triangles ( which would also of course scale up the size of my arrangement ).
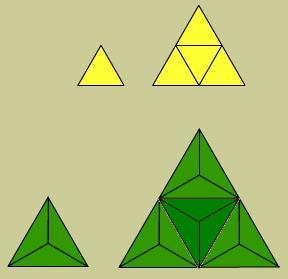
When working with green triangles the numbers follow the sequence: 3, 12, 27, 48 . . . 3b ² where b is the number in the sequence.
Which means I'm looking for a value of a and of b so that a ² = 3b ²
Keeping in mind that a and b are whole numbers ( a position in a sequence ) , a ² would have to have a factor of 3 to match 3b ² , but any factor a ² has it will have twice because it's a number squared. So a ² can only contain an even numbers of 3 s in its prime factors and 3b ² can only contain an odd numbers of 3 s. This means that a ² and 3b ² are never going to match, and an equilateral arrangements made from yellow triangles is never going to match an equilateral arrangements made from green triangles
Equal Equilateral Triangles
Age 14 to 16
Challenge Level 
The screen shot on the Hints page shows some solution arrangements.
When we looked at the solutions sent in, some people had started by putting triangles together until they could make a hexagon, others started with a hexagon and looked for ways it might split up into the two types of triangle.
Well done to Daniel from Royston and to Georgina from St. George's School for seeing the answer to the first important question :
'Did that tell you something about yellow and green triangles, about how they relate to each other' ?
Two yellow triangles make a rhombus of a size which can also be made by two green triangles.
And that lets us see that the yellow and green hexagons are equal because the yellow and green triangles have the same area (half that rhombus) and both hexagons use six triangles. But the equilateral triangles (below) do not use the same number of triangles and so cannot be the same size.
Esther had a great approach using sequences :
You can make equilateral triangle arrangements from yellow triangles :
The numbers needed follow the sequence : 1, 4, 9, 16 . . . a ² where a is the number in the sequence.
When I tried making equilateral triangles with the green triangles I could see that one way to do it was by replacing each equilateral space with three green triangles ( which would also of course scale up the size of my arrangement ).
When working with green triangles the numbers follow the sequence: 3, 12, 27, 48 . . . 3b ² where b is the number in the sequence.
Which means I'm looking for a value of a and of b so that a ² = 3b ²
Keeping in mind that a and b are whole numbers ( a position in a sequence ) , a ² would have to have a factor of 3 to match 3b ² , but any factor a ² has it will have twice because it's a number squared. So a ² can only contain an even numbers of 3 s in its prime factors and 3b ² can only contain an odd numbers of 3 s. This means that a ² and 3b ² are never going to match, and an equilateral arrangements made from yellow triangles is never going to match an equilateral arrangements made from green triangles
This is great reasoning, but how do we know that replacing each equilateral space with three green triangles is the only way to build up to an equilateral triangle ?We hope you enjoy the brain-stretching this kind of reasoning involves.Be encouraged, students a lot older than Stage 4 still wrestle with this sort of thinking.
