Repeating Patterns

Repeating Patterns

Have a go at making these repeating patterns:

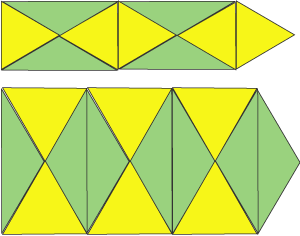
You could use the interactivity below to try out your ideas, or you could print off these sheets of triangles on coloured paper.

Try continuing the patterns. How did you know where to place the triangles?

What other repeating patterns can you make with these triangles?
 

Please send us some pictures of your creations.

Why do this problem?

This problem offers children the opportunity to recognise, make and describe repeating patterns of triangles, and then challenges them to create repeating patterns of their own.

This task is a great context in which to develop mathematical flexibility through geometry, and you can read more in this article.

Possible approach

Using the interactivity, or cut-out triangles on the floor/board, you could begin to make the first pattern for the group to see. Ask children to work in pairs to make the same pattern and continue it, using the interactivity on a tablet or computer, or using cut-out coloured triangles. (You may like to print off these sheets of the triangles onto coloured paper or card.)

Invite one pair to come to the board to continue the pattern and discuss with the whole class how they knew what to do. Encourage children to articulate the repetition of the two yellow and two green triangles making a rectangle. (Referring to the colours of the shapes rather than their names may be more appropriate for some.) Listen out for different ways of describing the repetition - there is not just one 'right' way.

A plenary could consist of sharing a few of the class' patterns, again focusing on how we know how to continue them. You could do this by starting the pattern and then continuing it wrongly, to see whether the children can correct you.

Key questions

Can you tell me about the pattern?
How would you carry on this pattern?
How do you know?

Possible support

Some children might find it helpful to have more examples of patterns to continue before creating their own.

Possible extension

Children could be offered other shapes to use in creating patterns in addition to the two triangles here. For example, a triangle which is half the size of each could be used as well.