Skip over navigation
This is a number spinner. When you spin it, it can land on any number from one to ten.
Here are three more number spinners with ten numbers on them. But you cannot see what the numbers are.
I spun the red one $15$ times and got these numbers:
I spun the blue one $15$ times and the yellow one $15$ times and got these numbers:
Then I did the same things again twice over. I got these numbers, but forgot to note which numbers came from which spinner:
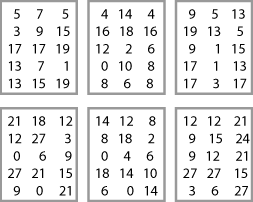
Can you work out which spinner generated each list? How did you do it?
We could call the numbers on the first spinner "Numbers from one to ten".
Can you think of a title for the set of numbers on the red spinner?
Can you think of titles for the sets of numbers on the blue and the yellow spinners?
Three Spinners
Age 7 to 11
Challenge Level 
Three Spinners
This is a number spinner. When you spin it, it can land on any number from one to ten.
Here are three more number spinners with ten numbers on them. But you cannot see what the numbers are.
I spun the red one $15$ times and got these numbers:
Then I did the same things again twice over. I got these numbers, but forgot to note which numbers came from which spinner:
Can you work out which spinner generated each list? How did you do it?
We could call the numbers on the first spinner "Numbers from one to ten".
Can you think of a title for the set of numbers on the red spinner?
Can you think of titles for the sets of numbers on the blue and the yellow spinners?
Why do this problem?
This problem challenges children to find a relationship between sets of numbers and introduces them to the idea of random events. It provides a reason to be able to scan a list which is something that some learners find quite difficult.
Possible approach
This problem could follow a series of lessons on number properties, or it could be used prior to some number work to assess your children's knowledge. In order to have a go at it, they will not need to have encountered probability before.
The activity might be best introduced orally, with just the lists of numbers displayed on the board. It would also be useful for pairs to have a copy of the resource sheet which contains all nine lists. Try not to say too much about what they might do to solve the problem -
leave them to develop their own method in their pairs. Warn them that you will expect them to explain what they did.
In a plenary discussion, focus on how the children came to their conclusions. Challenge them to explain why each spin of, for example, the yellow spinner, didn't produce exactly the same numbers.
Key questions
What can you tell me about these numbers?
What do these numbers have in common?
Which other card has these numbers?
Possible extension
Some learners can be asked to make spinners of their choice and write their own problem. Is there anything they can do to make the challenge as hard as possible? This would be a good discussion point afterwards.
Possible support
Using the resource sheet , some children might find it useful to cut out the lists of numbers and physically put the similar ones together.
You may also like
Roll These Dice
Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?
Bipin's Choice
Bipin is in a game show and he has picked a red ball out of 10 balls. He wins a large sum of money, but can you use the information to decided what he should do next?
Trick or Treat
Mrs. Smith had emptied packets of chocolate-covered mice, plastic frogs and gummi-worms into a cauldron for treats. What treat is Trixie most likely to pick out?