Skip over navigation
Can't Find a Coin?
Age 11 to 14
Challenge Level 
Imagine your teacher has set you the homework task of throwing a coin 100 times and carefully recording your results in the order that they appear. Imagine that you can't be bothered to go and find a coin - the task is just too tedious. So you decide to try to fool your teacher.
How will you go about it?
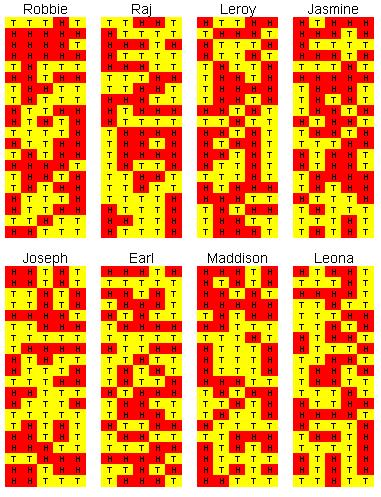
One of these students made up their homework results, which one is the most suspicious?
BACKGROUND INFORMATION
Whilst all combinations of Heads and Tails are equally likely, certain sets of results (such as all heads or alternating Heads and Tails all the way) would look rather suspicious. Why is this?
The computer here is programmed to determine whether the set of Heads and Tails falls into a suspicious category or not. Rather interestingly, if you do generate the Heads and Tails truly randomly using a coin then there is a 95% chance the the computer will know that these were generated randomly. Don't believe it? Try it out!
How will you go about it?
One of these students made up their homework results, which one is the most suspicious?
BACKGROUND INFORMATION
Whilst all combinations of Heads and Tails are equally likely, certain sets of results (such as all heads or alternating Heads and Tails all the way) would look rather suspicious. Why is this?
The computer here is programmed to determine whether the set of Heads and Tails falls into a suspicious category or not. Rather interestingly, if you do generate the Heads and Tails truly randomly using a coin then there is a 95% chance the the computer will know that these were generated randomly. Don't believe it? Try it out!
You may also like
Stop or Dare
All you need for this game is a pack of cards. While you play the game, think about strategies that will increase your chances of winning.
Snail Trails
This is a game for two players. Does it matter where the target is put? Is there a good strategy for winning?
Game of PIG - Sixes
Can you beat Piggy in this simple dice game? Can you figure out Piggy's strategy, and is there a better one?