Skip over navigation
Article by Toni Beardon
There are two versions of this article, this one is complete and the other 'challenge' version has blanks for the reader to fill in.
This is the first of a series of articles on mathematical logic which will show that truth tables, set theory, Boolean algebra and electronic circuits are essentially equivalent; that is, theorems that can be proved in one system have their counterparts in the other systems. In subsequent articles we shall see how Boolean algebra is used in designing electronic circuits. In this article we begin to explore the links between electronic circuits and mathematical logic.
Although logic does not model language perfectly it does form a useful system that, in practice, is the basis of most of the communication of mathematical ideas between working mathematicians. Logical conventions are used to overcome the ambiguities and inadequacies of language. The philosophical aspects of the subject are rather more subtle and complicated and we shall not dwell on them.
A proposition is a statement that has exactly one of the truth values 'true' or 'false'. A propositional function is a sentence involving variables, for example "She is the Queen of England" and "x is greater than 7". These functions become propositions when meanings are substituted for the variables ('she' and 'x' in the above examples).
Before we go on to experiment with circuits we need a notation to record and summarize the combinations of propositions used in logical arguments and also the combinations of switches used in circuits.
We use small letters $p, q, r...$ to represent propositions. If the proposition $p$ is true it is said to have the truth value 1 (or sometimes T) and if false the truth value 0 (or F). Propositional logic is concerned with compound propositions formed from given propositions by means of the connectives 'not', 'and', 'or', 'if ... then' and combinations of these connectives, for example 'if and only if'.
In circuit diagrams each switch is either 'on' (representing the number 1) or 'off' (representing the number 0). Combinations of switches called {\it logical gates} represent the logical {\it connectives}.
Logical arguments are a combination of propositions, and circuits are a combination of switches that control the flow of current. Modern computers not only store data in the form of '0's and '1's, on which they perform arithmetic, but perform many highly complex tasks that we have come to take for granted. Studying the relation between truth tables and circuits will help us to understand a little of the underlying principles behind the design and programming of computers.
{\bf Negation}
Now it is time to use Design your own circuit to make some of your own circuits and find out how the logic gates work.
Given a proposition $p$, the {\it negation} not-$p$, written $\neg p$, is the proposition demonstrated by this circuit and defined by the following truth table. $$ \begin{array}[t]{cc} p & \neg p \\ 1 & 0 \\ 0 & 1 \end{array} $$
Conjunction
The logical connective 'and' is used to make a compound proposition from two component propositions. For example if we speak the truth when we say "Today is Friday and it is raining" then both of the component propositions are true. If either or both are false then the compound proposition is false.
Disjunction
In everyday language we often use 'or' inclusively as in "If you want to buy cereals or soft drinks go to aisle 7 in the supermarket" when we expect people who want to buy both cereals and soft drinks to go to that aisle as well as people wanting to buy just one of them. On other occasions we use 'or' exclusively to offer two alternatives expecting the listener to choose just one of them as in "Do you want steak for dinner or chicken?". The meaning is usually clear from the context but to avoid any ambiguity in mathematics the logical connective 'or' is always used inclusively and never exclusively.
Given any two propositions $p$ and $q$ the disjunction $p$ or $q$, (written $p \vee q$)is given in the following truth table.
Compound propositions
Truth tables for more complicated compound propositions can be formed from the simpler ones. For example, the following truth table and circuit (Fig 5) show that $\neg(p\vee q)$ has the same truth values as $\neg p \wedge \neg q$.
The following truth table and Fig. 6 show that $\neg (p\wedge q)$ is equivalent to $\neg p \vee \neg q$.
XOR, NAND, NOR and XNOR
Next we investigate some of the other logical gates used in circuitry. Then we shall discuss other important logical connectives such as 'implies', often expressed as 'if... then' as in "if I go to the shops then I'll buy you some ice-cream". After that we shall be able to relate the circuits to the language of logical arguments and also see how circuits can be built to perform simple operations such as addition.
Now experimenting with the circuits for XOR, NAND, NOR and XNOR the following truth table can be filled in. $$ \begin{array}[t]{cc} p &q &p XOR q & p NAND q &p NOR q & p XNOR q \\ 1 &1 &0 &0 &0 &1 \\ 1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &0 \\ 0 &0 &0 &1 &1 &1 \\ \end{array} $$ Comparing these tables to what we have already discovered we see that p NOR q means 'not(p or q)', that is $\neg (p\vee q)$, and it is also equivalent to $\neg p \wedge \neg q$.\par Also p NAND q means 'not(p and q)', that is $\neg (p\wedge q)$, and it is also equivalent to $\neg p \vee \neg q$.
Implication
Thinking about what we mean by 'if p then q' we see that this rules out the possibility that p is true and q is false. If I make the promise " if I go to the shops then I'll buy you some ice-cream" but I go to the shop and do not buy the ice-cream then I have broken my promise. So, denoting 'if p then q' by $p \Rightarrow q$, the truth table for 'if p then q' must include the line: $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &0 &0 \\ \end{array} $$ As the following example shows true conclusions can be proved by valid arguments from false premises and so we should expect 'false $\Rightarrow$ true' to be true.\par We shall prove the proposition '2=1 $\Rightarrow$ 2=2'. Of course 2=2 is true (by definition) but the following argument proves this as a consequence of a false hypothesis.\par By the symmetry of equality if 2=1 then 1=2. By the transitivity of equality it follows that, having shown 2=1 and 1 = 2, then 2 = 2.\par This establishes a second line in the truth table for implication. $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &0 &0 \\ 0 &1 &1 \\ \end{array} $$ There might still be some doubt in the reader's mind about why the definition of 'false' implies 'true' is 'true'. It could not be false because then we would have $p \Rightarrow q$ logically the same as $q\Rightarrow p$ which is not the case. Consider for example $x=1 \Rightarrow x> 0$ which is true whereas $x> 0 \Rightarrow x=1$ is false, so we have no choice but to make this definition for $p \Rightarrow q$.\par Also 'if x then x' is true whether x is true or false so we must have the complete truth table as follows. $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &1 \\ 0 &0 &1 \\ \end{array} $$ It is convenient to have a single connective which combines $p \Rightarrow q$ and $q \Rightarrow p$. This connective is the {\it bi-conditional} 'p if and only if q' (written $p \Leftrightarrow q$)and defined by the truth table: $$ \begin{array}[t]{cc} p &q &$p\Leftrightarrow q$ \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{array} $$ We observe that in the truth table for $p \Leftrightarrow q$ this compound proposition is true precisely in those circumstances in which p and q have the same truth values and this is given by the logic gate p XNOR q. Also observe that the logic gate p XOR q is equivalent to $\neg(p \Leftrightarrow q)$.
Note that p XOR q is 'the exclusive or', true when either p is true or when q is true but not when they are both true. In everyday language we often use the exclusive or, as in "do you want steak or chicken for dinner?", but to the mathematician who, by convention, uses only the inclusive or, the logical answer is " yes" if he wants meat for dinner and "no" if he does not want meat.
Tautologies
If the truth value of a compound proposition is always true for all possible combinations of truth values of the given propositions, then the compound proposition is called a tautology. The following truth table and circuit show that $p \vee \neg p$ is a tautology. This is called the Law of the Excluded Middle because either $p$ is true or $\neg p$ is true and there is no third alternative.
The Sheffer stroke
The five connectives $\neg, \wedge, \vee, \Rightarrow, \Leftrightarrow$ can be defined in terms of one symbol called the Sheffer stroke which was devised by H.M.Sheffer in 1913. At the time it was simply a piece of pure mathematics, but later it has had applications in designing electronic circuits from assemblies of a single component, the NAND gate. We have already seen that p NAND q is equivalent to 'not (p and q)' or, equivalently, 'not p or not q' and that it has the following truth table. $$ \begin{array}[t]{cc} p &q &p NAND q \cr && Sheffer stroke \cr 1 &1 &0 \cr 1 &0 &1 \cr 0 &1 &1 \cr 0 &0 &1 \cr \end{array} $$
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 11 to 18
Logic, Truth Tables and Switching Circuits
Introduction
If you want a very simple introduction to truth tables you might like to start with Truth Tables and Electronic Circuits but this article does not assume any prior knowledge of truth tables or circuits.
There are two versions of this article, this one is complete and the other 'challenge' version has blanks for the reader to fill in.
 |
In this article you will find explanations of circuits and how they correspond to the logical language we use to discuss mathematics. You will be challenged to summarise the workings of the circuits by filling in blanks in the corresponding truth tables. At any time you can switch to this version of the article to check your answers. |
This is the first of a series of articles on mathematical logic which will show that truth tables, set theory, Boolean algebra and electronic circuits are essentially equivalent; that is, theorems that can be proved in one system have their counterparts in the other systems. In subsequent articles we shall see how Boolean algebra is used in designing electronic circuits. In this article we begin to explore the links between electronic circuits and mathematical logic.
Although logic does not model language perfectly it does form a useful system that, in practice, is the basis of most of the communication of mathematical ideas between working mathematicians. Logical conventions are used to overcome the ambiguities and inadequacies of language. The philosophical aspects of the subject are rather more subtle and complicated and we shall not dwell on them.
A proposition is a statement that has exactly one of the truth values 'true' or 'false'. A propositional function is a sentence involving variables, for example "She is the Queen of England" and "x is greater than 7". These functions become propositions when meanings are substituted for the variables ('she' and 'x' in the above examples).
Before we go on to experiment with circuits we need a notation to record and summarize the combinations of propositions used in logical arguments and also the combinations of switches used in circuits.
We use small letters $p, q, r...$ to represent propositions. If the proposition $p$ is true it is said to have the truth value 1 (or sometimes T) and if false the truth value 0 (or F). Propositional logic is concerned with compound propositions formed from given propositions by means of the connectives 'not', 'and', 'or', 'if ... then' and combinations of these connectives, for example 'if and only if'.
In circuit diagrams each switch is either 'on' (representing the number 1) or 'off' (representing the number 0). Combinations of switches called {\it logical gates} represent the logical {\it connectives}.
Logical arguments are a combination of propositions, and circuits are a combination of switches that control the flow of current. Modern computers not only store data in the form of '0's and '1's, on which they perform arithmetic, but perform many highly complex tasks that we have come to take for granted. Studying the relation between truth tables and circuits will help us to understand a little of the underlying principles behind the design and programming of computers.
{\bf Negation}
Now it is time to use Design your own circuit to make some of your own circuits and find out how the logic gates work.
| First, connect a switch to a lamp as in Fig. 1 and click on the switch several times to change it from 1 to 0 and back to 1. Observe that the light goes on when the switch registers 1 and the light goes off when the switch registers 0. |
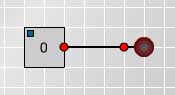 Fig. 1
|
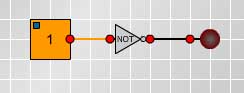 Fig. 2
|
Now put a NOT gate into the circuit between the switch and the lamp, as shown in Fig. 2, and observe what happens when you change the switch from 1 to 0. |
Given a proposition $p$, the {\it negation} not-$p$, written $\neg p$, is the proposition demonstrated by this circuit and defined by the following truth table. $$ \begin{array}[t]{cc} p & \neg p \\ 1 & 0 \\ 0 & 1 \end{array} $$
Conjunction
The logical connective 'and' is used to make a compound proposition from two component propositions. For example if we speak the truth when we say "Today is Friday and it is raining" then both of the component propositions are true. If either or both are false then the compound proposition is false.
| Make and test the circuit shown in Fig 3. The truth table summarises the workings of this circuit. |
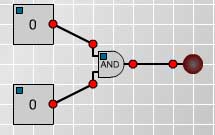 Fig. 3 Fig. 3 |
$$ \begin{array}[t]{cc} p &q &$p\wedge q$ \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &0 \\ \end{array} $$ |
Disjunction
In everyday language we often use 'or' inclusively as in "If you want to buy cereals or soft drinks go to aisle 7 in the supermarket" when we expect people who want to buy both cereals and soft drinks to go to that aisle as well as people wanting to buy just one of them. On other occasions we use 'or' exclusively to offer two alternatives expecting the listener to choose just one of them as in "Do you want steak for dinner or chicken?". The meaning is usually clear from the context but to avoid any ambiguity in mathematics the logical connective 'or' is always used inclusively and never exclusively.
Given any two propositions $p$ and $q$ the disjunction $p$ or $q$, (written $p \vee q$)is given in the following truth table.
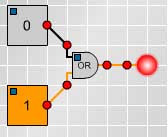 Fig.4
|
Make the circuit shown in Fig 4. for the connective 'or'. Check your results with the truth table on the right. | $$ \begin{array}[t]{cc} p &q &$p\vee q$ \\ 1 &1 &1\\ 1 &0 &1\\ 0 &1 &1\\ 0 &0 &0 \\ \end{array} $$ |
Compound propositions
Truth tables for more complicated compound propositions can be formed from the simpler ones. For example, the following truth table and circuit (Fig 5) show that $\neg(p\vee q)$ has the same truth values as $\neg p \wedge \neg q$.
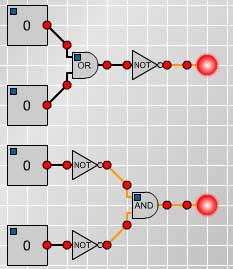 Fig. 5
|
$$ \begin{array}[t]{cc} p &q &$p\vee q$ &$\neg (p\vee q)$ &$\neg p$ &$\neg q$ & $\neg p \wedge \neg q$ \\ 1 &1 &1 &0 &0 &0 &0 \\ 1 &0 &1 &0 &0 &1 &0 \\ 0 &1 &1 &0 &1 &0 &0 \\ 0 &0 &0 &1 &1 &1 &1 \\ \end{array} $$ |
| $$ \begin{array}[t]{cc} p &q &$p\wedge q$ &$\neg (p\wedge q)$ &$\neg p$ &$\neg q$ & $\neg p \vee \neg q$ \\ 1 &1 &1 &0 &0 &0 &0 \\ 1 &0 &0 &1 &0 &1 &1 \\ 0 &1 &0 &1 &1 &0 &1 \\ 0 &0 &0 &1 &1 &1 &1 \\ \end{array} $$ |
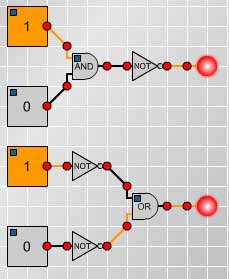 Fig. 6
|
Next we investigate some of the other logical gates used in circuitry. Then we shall discuss other important logical connectives such as 'implies', often expressed as 'if... then' as in "if I go to the shops then I'll buy you some ice-cream". After that we shall be able to relate the circuits to the language of logical arguments and also see how circuits can be built to perform simple operations such as addition.
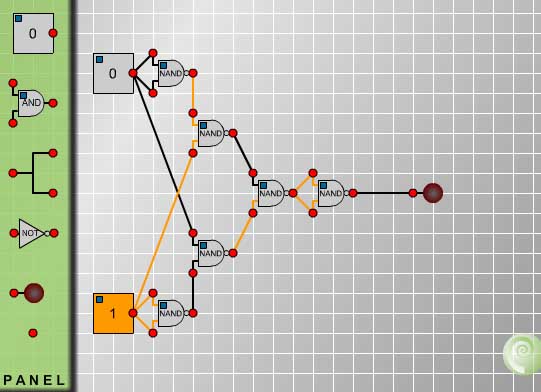
Now experimenting with the circuits for XOR, NAND, NOR and XNOR the following truth table can be filled in. $$ \begin{array}[t]{cc} p &q &p XOR q & p NAND q &p NOR q & p XNOR q \\ 1 &1 &0 &0 &0 &1 \\ 1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &0 \\ 0 &0 &0 &1 &1 &1 \\ \end{array} $$ Comparing these tables to what we have already discovered we see that p NOR q means 'not(p or q)', that is $\neg (p\vee q)$, and it is also equivalent to $\neg p \wedge \neg q$.\par Also p NAND q means 'not(p and q)', that is $\neg (p\wedge q)$, and it is also equivalent to $\neg p \vee \neg q$.
Implication
Thinking about what we mean by 'if p then q' we see that this rules out the possibility that p is true and q is false. If I make the promise " if I go to the shops then I'll buy you some ice-cream" but I go to the shop and do not buy the ice-cream then I have broken my promise. So, denoting 'if p then q' by $p \Rightarrow q$, the truth table for 'if p then q' must include the line: $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &0 &0 \\ \end{array} $$ As the following example shows true conclusions can be proved by valid arguments from false premises and so we should expect 'false $\Rightarrow$ true' to be true.\par We shall prove the proposition '2=1 $\Rightarrow$ 2=2'. Of course 2=2 is true (by definition) but the following argument proves this as a consequence of a false hypothesis.\par By the symmetry of equality if 2=1 then 1=2. By the transitivity of equality it follows that, having shown 2=1 and 1 = 2, then 2 = 2.\par This establishes a second line in the truth table for implication. $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &0 &0 \\ 0 &1 &1 \\ \end{array} $$ There might still be some doubt in the reader's mind about why the definition of 'false' implies 'true' is 'true'. It could not be false because then we would have $p \Rightarrow q$ logically the same as $q\Rightarrow p$ which is not the case. Consider for example $x=1 \Rightarrow x> 0$ which is true whereas $x> 0 \Rightarrow x=1$ is false, so we have no choice but to make this definition for $p \Rightarrow q$.\par Also 'if x then x' is true whether x is true or false so we must have the complete truth table as follows. $$ \begin{array}[t]{cc} p &q &$p \Rightarrow q$ \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &1 \\ 0 &0 &1 \\ \end{array} $$ It is convenient to have a single connective which combines $p \Rightarrow q$ and $q \Rightarrow p$. This connective is the {\it bi-conditional} 'p if and only if q' (written $p \Leftrightarrow q$)and defined by the truth table: $$ \begin{array}[t]{cc} p &q &$p\Leftrightarrow q$ \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{array} $$ We observe that in the truth table for $p \Leftrightarrow q$ this compound proposition is true precisely in those circumstances in which p and q have the same truth values and this is given by the logic gate p XNOR q. Also observe that the logic gate p XOR q is equivalent to $\neg(p \Leftrightarrow q)$.
Note that p XOR q is 'the exclusive or', true when either p is true or when q is true but not when they are both true. In everyday language we often use the exclusive or, as in "do you want steak or chicken for dinner?", but to the mathematician who, by convention, uses only the inclusive or, the logical answer is " yes" if he wants meat for dinner and "no" if he does not want meat.
Tautologies
If the truth value of a compound proposition is always true for all possible combinations of truth values of the given propositions, then the compound proposition is called a tautology. The following truth table and circuit show that $p \vee \neg p$ is a tautology. This is called the Law of the Excluded Middle because either $p$ is true or $\neg p$ is true and there is no third alternative.
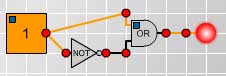 Fig. 7
|
$$ \begin{array}[t]{cc} p &$\neg p$ &$p \vee \neg p$ \\ 1 &0 &1 \\ 0 &1 &1 \\ \end{array} $$ |
The Sheffer stroke
The five connectives $\neg, \wedge, \vee, \Rightarrow, \Leftrightarrow$ can be defined in terms of one symbol called the Sheffer stroke which was devised by H.M.Sheffer in 1913. At the time it was simply a piece of pure mathematics, but later it has had applications in designing electronic circuits from assemblies of a single component, the NAND gate. We have already seen that p NAND q is equivalent to 'not (p and q)' or, equivalently, 'not p or not q' and that it has the following truth table. $$ \begin{array}[t]{cc} p &q &p NAND q \cr && Sheffer stroke \cr 1 &1 &0 \cr 1 &0 &1 \cr 0 &1 &1 \cr 0 &0 &1 \cr \end{array} $$
Related Collections
You may also like
Flow Chart
The flow chart requires two numbers, M and N. Select several values for M and try to establish what the flow chart does.

