Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Balance Power



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
There was a lot of interest and a big response to this problem. However finding an answer should prompt the questions: "Why does this happen?" , "Can I explain and prove it?", "Can the result be proved for ALL values of n?" This question remains a Tough Nut and the challenge is to prove that the method using both scale pans always works.
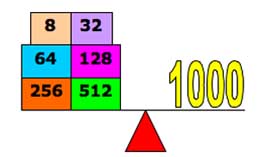 Thank you to Phil of Garforth Community College for this diagram. |
This is a solution to the first part from Jeremy of Taunton
Prep School.
All numbers can be expressed in Base 2 (Binary) as a sum of
powers of 2, written using only the digits 1 or 0.
Objects of integer mass up to 60 (indeed up to 63, for 63 =
2^6 - 1), can all be balanced by combinations using a maximum of
one of each of the following weigths: 1, 2, 4, 8, 16 and 32
units.
Objects of integer mass up to 1000 units (in fact up to 1023
units) can all be balanced by combinations using a maximum of one
of each of 10 different weights, as
$2^9 < 1000 < 2^{10}.$
Therefore, the number of different weights (w) needed to weigh
up to n units is related to the number (n), by the
expression:
$2^{w-1} \leq n < 2^w$. |
Can you prove the following result which was spotted by Chanwc from Hong Kong and Utku Alhan from Robert College of Istanbul who realised that the number of weights is given by:
$w = [(log n)/(log 2)] + 1 $ where the square brackets $[\ ]$ means 'the integer part of' and the weights are $2^0, 2^1, ..., 2^{w-1}$.
It remains to prove that the folllowing method, described by Joris from Claremont High School, will always work for all n.
If it is possible to put weights on both sides, you only need to use powers of 3. The first weight is worth 1, the second worth 3. You can form 1 (1), 2 by putting 3 on one side and 1 on the other (3-1). The maximum weight you can form is 6 (1+2+3). Instead of taking 7, you only need a weight worth 9, so you can form 7 (9-2) and 8 (9-1). This goes further, and to form all integers between 1 and 60, you only need 5 weights, 1, 3, 9, 27, 81.You may also like
Arrow Arithmetic 1
The first part of an investigation into how to represent numbers using geometric transformations that ultimately leads us to discover numbers not on the number line.
A Story about Absolutely Nothing
This article for the young and old talks about the origins of our number system and the important role zero has to play in it.

