Skip over navigation
Here's a couple of nice explanations :
From Francesca at Wimbledon High School : by the end of that week, the $40$ marked fish would have spread out and integrated with the rest of the fish population. So that the second lot of $40$ fish that are caught would be a thoroughly mixed group of marked and unmarked fish.
Count the number of marked and unmarked fish, get a ratio, then reason like this :
For example if in the second lot of $40$ fish, the marked to unmarked ratio was $2 : 38$ and we know that there are $40$ marked fish altogether, we might assume that the ratio in the second lot of fish is close to the ratio for all the fish together.
So $2 : 38$ matches $40 : ?$
$40/2$ is $20$ and then scaling that up by $38$ to get $760$ ($20\times38$)
And just to make sure...
$$38/2=19 $$
$$760/40=19 $$
then, we must add that ratio together:
$$40+760=800$$
Hey presto!!! There are $800$ fish altogether!
Thanks Francesca.
And from Stephen at Blatchington Mill School :
If you mark $40$ fish and release them. Then, when those fish have had time to mix back in with the whole population, catch another $40$. If you count the number ($c$) in that second catch which are already marked, you can estimate the size of the whole population ($T$) by saying that $40 = T(c/40) $
For example if when you looked at the second catch and $10$ were already marked then you could estimate that you had marked a quarter of the entire population of fish, because that's the proportion in the sample, so the original $40$ were about one quarter of the whole population and there are therefore approximately $120$ fish.
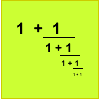
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Counting Fish
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here's a couple of nice explanations :
From Francesca at Wimbledon High School : by the end of that week, the $40$ marked fish would have spread out and integrated with the rest of the fish population. So that the second lot of $40$ fish that are caught would be a thoroughly mixed group of marked and unmarked fish.
Count the number of marked and unmarked fish, get a ratio, then reason like this :
For example if in the second lot of $40$ fish, the marked to unmarked ratio was $2 : 38$ and we know that there are $40$ marked fish altogether, we might assume that the ratio in the second lot of fish is close to the ratio for all the fish together.
So $2 : 38$ matches $40 : ?$
$40/2$ is $20$ and then scaling that up by $38$ to get $760$ ($20\times38$)
And just to make sure...
$$38/2=19 $$
$$760/40=19 $$
then, we must add that ratio together:
$$40+760=800$$
Hey presto!!! There are $800$ fish altogether!
Thanks Francesca.
And from Stephen at Blatchington Mill School :
If you mark $40$ fish and release them. Then, when those fish have had time to mix back in with the whole population, catch another $40$. If you count the number ($c$) in that second catch which are already marked, you can estimate the size of the whole population ($T$) by saying that $40 = T(c/40) $
For example if when you looked at the second catch and $10$ were already marked then you could estimate that you had marked a quarter of the entire population of fish, because that's the proportion in the sample, so the original $40$ were about one quarter of the whole population and there are therefore approximately $120$ fish.
You may also like
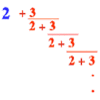
There's a Limit
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?
Not Continued Fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers?

