Tiling

Alex, Ayali, Brodie and Keya from Strand on the Green Primary School sent the following:

We decided the easiest way was to start with the biggest tiles that could fit

  

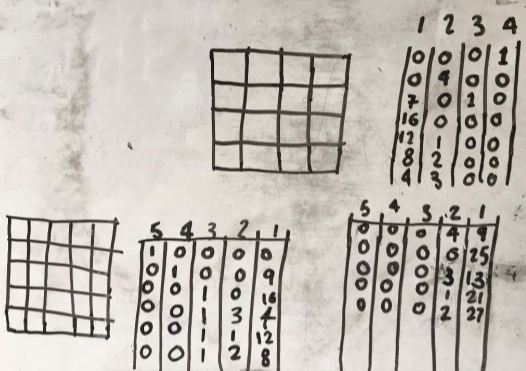
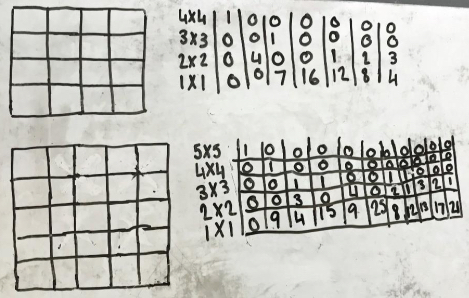
We agreed there are 7 possibilities for the 4 by 4 square and 11 for the 5 by 5 square. Initially that looks like a sequence adding 4 each time. However there are already 7 possible totals for the 6 by 6 square using the 6x6, 5x5 and 4x4 tiles so there will definitely be more than 15 (but we didn't have time to find them all).


Students from the International School of Brussels sent in their work:



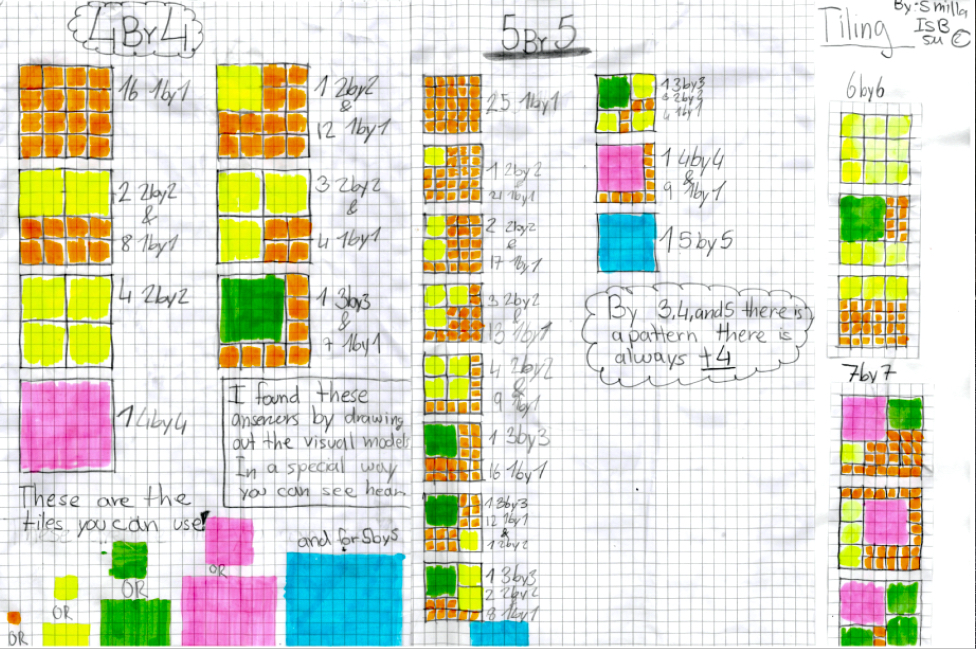
So, both submissions thought that the +4 from one size to another was a particular point of interest and maybe a rule?
Well done both sets of pupils.