Skip over navigation

Two-digit Targets

Age 5 to 7

Challenge Level Yellow star

Primary curriculum

Two-digit Targets

Two-digit Targets printable sheet

You have a set of the digits from $0$ - $9$.

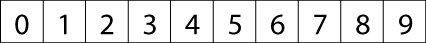
Can you arrange these digits in the five boxes below to make two-digit numbers as close to the targets as possible? You may use each digit once only.

How will you know that your solution is as close to the targets as possible?

You could use this interactivity to try out your ideas.

This activity has been adapted from one of BEAM's free Maths of the Month resources, which unfortunately are no longer available.

Printable NRICH Roadshow resource.

Why do this problem?

This problem is a fantastic opportunity for learners to apply knowledge of place value and offers a context for learning and practising the relevant vocabulary (odd, even, multiple). The interactivity will help learners satisfy their curiosity in the sense of finding a 'better' solution, as it enables them to play around with the digits without having to commit anything to paper. This act of deciding whether one solution is better than another also provides a meaningful context in which to compare and order numbers.

Possible approach

You could start by having two different digits and asking how the digits could be arranged to make the number that is the larger/smaller. Try this several times with different combinations of two digits. Could the digits be arranged to make a multiple of $5$? If not, why not?

Next you could introduce one of the criteria in the problem, such as making the largest possible even two-digit number. Alternatively, you could make up your own examples such as the largest even number or the nearest to $70$. You will need to establish whether $0$ can be used at the beginning of a number. This, in itself, can form an interesting discussion point. (The final decision itself does not matter - it is the reasons that are important, and the fact that the children feel as if it is their decision!)

Give pairs time to continue working on this problem, using the interactivity and/or a set of digit cards. Pairs may find this sheet useful for recording their thinking.

In the plenary, facilitate a general discussion on the strategies learners used to tackle the task and how they determined how 'good' a solution was.

Key questions

What have you tried so far?
What do you know about odd numbers/even numbers/multiples of 5? How does this help you place the digits?
Can you create a 'better' solution? How will you know it is better?

Possible extension

Some children might like the challenge of this four-digit version of the task.

Possible support

Making the numbers one at a time with set of $0$ - $9$ digit cards, or using the interactivity, should help all children access this problem.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Two-digit Targets

Two-digit Targets

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

I'm Eight

Let's Investigate Triangles

Noah