Brimful

Mark from Gozo College sent in a solution to this long problem



Brimful Finding constants A, B, C, D:


At (2.5, 10):

$Y=Ax: \quad A = y/x = 10/2.5 = 4$

$Y=Bx^2: \quad B=y/x^2 = 10/2.5^2 = 1.6$

$Y=Cx^3:\quad C=y/x^3 = 10/2.5^3 = 0.64$

$Y=Dx^4 + x: \quad D=(y-x)/x^4 = (10-2.5)/2.5^4 = 0.192$

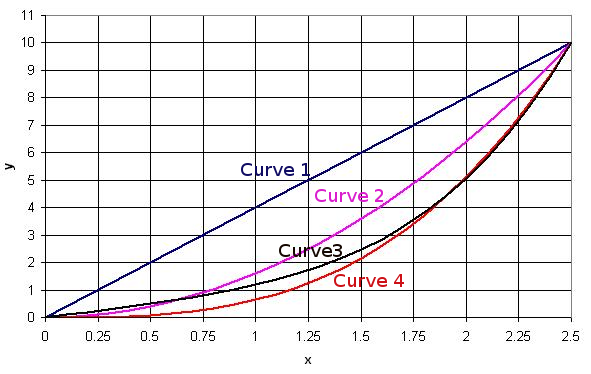
Matching equations to the graphs: At $x=1$

$Y=4x:\quad Y=4(1)=4$ Blue graph

$Y=1.6x^2:\quad Y=1.6(1)^2 = 1.6$ \pink graph

$Y=0.64x^3:\quad Y=0.64(1)^3 = 0.64$ Red graph

$Y=0.192x^4+x:\quad Y = 0.192(1)^4 + (1)$ Black graph

Volume of Revolution of Blue graph around $x=0$

$Y=Ax$

$X=y/A$

Cross-sectional area of volume at any $y$ is

$\pi(x)^2 =\pi(y/A) ^2$

Volume of revolution

= sum of the area of an infinite number of circular cross-sections with 0 thickness

= integral of $\pi(y/A) ^2$ for the graph between y=0 and y=h, where h = height of vessel

= $\pi(h^3)/(3A^2)$

=$\pi(10^3)/(3(4)^2)$

Substituting $h = 10, A = 4$ gives $65.4cm^3$

Volume of Revolution of pink graph around$ x=0$

$Y=Bx^2$

$X=(y/B)^(1/2)$

Cross-sectional area of volume at any y is

$\pi(x)^2 =\pi(y/B)$

Volume of revolution = sum of the area of an infinite number of circular cross-sections with 0 thickness = integral of $\pi(y/B)$ for the graph between $y=0$ and $y=h$, where $h$ = height of vessel

$= \pi(h)^2 / (2B)$

$=\pi(10)^2/(2(1.6))$

Substituting $h = 10, B = 1.6$ gives $98.2cm^3$

Similarly, the volume of Revolution of Red graph is

$3\pi(h)^{5/3}/(5C^{2/3}) = 3\pi(10)^{5/3}/(5(0.64)^{2/3})$ Substituting $h = 10, C = 0.64$ gives $117.8cm^3$

Volume of Revolution of Black graph around $x=0$

$Y=Dx^4 + x$

This equation was hard to rearrange to make x subject so, the volume beneath the vessel formed by the revolution of $Y=Dx^4 + x$ around $x=0$ was found. Then this is subtracted from the volume of the cylinder of radius $s$ and height $Ds^4 + s$ to find the volume of the vessel.

The volume beneath the vessel is formed by an infinite number of hollow cylinders with radius x and height $Dx^4 + x$. The thickness of the wall of the cylinders is 0.

Therefore, the surface area SA of one side of such a cylinder is circumference times height

$=2\pi(x)(Dx^4 + x) =2\pi(Dx^5 + x^2)$

Volume beneath vessel of radius $s$

=sum of the SA of an infinite number of hollow concentric cylinders with 0 thickness

=integral of $2\pi(Dx^5 + x^2)$ for the graph between $x=0$ and $x=s$

$=\pi(s)^3(Ds^3 + 2)/3$


Volume of cylinder of radius s and height $h=Ds^4 + s$

$=\pi \times radius^2 \times h$

$=\pi(s)^3(Ds^3 + 1)$



Volume of vessel = Volume of cylinder minus Volume beneath vessel

$= \pi(s)^3(Ds^3 + 1) - \pi(s)^3(Ds^3 + 2)/3$

$=\pi\times s^3\times (2Ds^3 + 1)/3$

$=\pi\times (2.5)^3\times(2\times 0.192\times (2.5)^3 + 1)/3$

Substituting $s = 2.5, D=0.192$ gives $114.5cm^3$


Patrick from Woodbridge school also sent in his thoughts where he found the values of the constants and also used the formula for the volume of a cone to evaluate one of the integrals.

Constants ABCD are chosen so that the following 4 curves pass through the point $(2.5,10) $

$y=Ax \quad y=Bx^2 \quad y=Cx^3 \quad y=Dx^4+x$

The first observation I made is that all the curves pass through the origin.

Therefore, the first equation is easy: $y = Ax$, where $y = 10$ and $x = 2.5$, gives $10 = A\times 2.5$ so $A = 4$.

This is the only straight line on the graph.

$y = Bx^2$ where $y = 10$ and $x = 2.5$, gives $10 = B\times 6.25$, so $B = 1.6$.

$y = Cx^3$ where $y = 10$ and $x = 2.5$, gives $10 = C\times 15.625$, so $C = 0.64$.

$y = Dx4 + x$ where $y = 10$ and $x = 2.5$, gives $10 = D\times 39.0625 + 2.5$, so $7.5/39.0625 = D = 0.192$.

Seeing what point the graphs go through at $x = 1: y = Bx^2 = 1.6$ so is purple $y = Cx^3 = 0.64$ so is red $y = Dx^4 + x = 1.192$ so is black.

I shall call the shapes made by rotating the lines, A, B, C and D according to the coefficient of the highest power of x in the equation of the line.

Thus, shape A is a cone, with volume $pi r^2h/3$. This gives it a volume of $\pi \times 6.25\times 10/3 = 65.45 cm3$.







Simon's solutions was as follows:

Part 1:

Substitute $x = 2.5$ and $y =10$ into each equation and rearrange to find the values of the constants.

• $A = 4$
• $B = \frac{8}{5}$
• $C = \frac{16}{25}$
• $D = \frac{24}{125}$

Part 2:

For each equation substitue a series of $x$ values into the equation and tabulate the corresponding $y$ values. Then match the equation to the curve which gives the correct trajectory of points.

Note: one point should be sufficient to match the equation to the curve.

Curve 1	$y = 4x$	(as this is the only linear plot)
Curve 2	$y = \frac{8}{5} x^2$	(at $x = 2.25$ , $y = 1.6 \times 2.25^2 = 8.1$ which matches the pink curve)
Curve 3	$y = \frac{24}{125} x^4 + x$	( at $x =1$, $y = 1 + 0.192 = 1.192$ which matches the black curve)
Curve 4	$y = \frac{16}{25} x^3$	(at $x =1$, $y = 0.64$ which matches the red curve)

Part 3:

The volume generated by rotation about the y axis can be found by the method of shells or the method of discs, here we use the method of shells.

The method of shells is based upon filling the solid of revolution with an infinite number of thin cylindrical shells. The volume of each shell is equal to its circumference ($2 \pi x$) multiplied by its height $\left[ y = f(x) \right]$, by allowing the thickness of each shell to approach zero and summing all shells we obtain the definite integral for the volume of revolution $V_{rev}$

$$V_{rev} = \int 2 \pi \ x \ y \mathrm{\ d}x $$

The volume calculated via the method of shells will be the volume between $x$-axis, the curve and the line $x=2.5$ (when we rotate the curve about $y$).

The volume of the vessel $V_{vessel}$ can be found by subtracting the volume of revolution $V_{rev}$ from the volume of a cylinder of height $10 \mathrm{\ cm}$ and radius $2.5 \mathrm{\ cm}$.

$$V_{vessel} = (10 \times 2.5^2 \pi) - V_{rev} = \frac{125\pi}{2}- V_{rev}$$

Curve 1:

Volume generated by rotation about $y$

$$V_{rev} = \int_0^{2.5} 2\pi (x)(4x) \ \mathrm{d}x = 8\pi \left[\frac{1}{3}x^3 \right]^{2.5}_0 = \frac{8 \pi}{3} \times 2.5^3 =\frac{125 \pi}{3}$$ $$\Rightarrow V_{vessel} = \frac{125\pi}{2} - \frac{125 \pi}{3} = \frac{125 \pi}{6} = 65.45 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 2:

Volume generated by rotation about $y$

$$V_{rev} = \int_0^{2.5} 2\pi (x) \left( \frac{8}{5}x^2 \right) \ \mathrm{d}x = \frac{16\pi}{5} \left[ \frac{1}{4}x^4 \right]^{2.5}_0 = \frac{4 \pi}{5} \times 2.5^4 = \frac{125 \pi}{4}$$ $$\Rightarrow V_{vessel} = \frac{125\pi}{2} - \frac{125 \pi}{4} = \frac{125 \pi}{4} = 98.17 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 3:

Volume generated by rotation about $y$

$$V_{rev} = \int_0^{2.5} 2\pi (x) \left( \frac{24}{125}x^4 + x \right) \ \mathrm{d}x = 2\pi \left[ \frac{24}{125} \frac{1}{6}x^6 + \frac{1}{3}x^3 \right]^{2.5}_0 = \left(\frac{8}{125} \times 2.5^6 + \frac{2}{3} \times 2.5^3 \right) \pi = \frac{625 \pi}{24}$$ $$\Rightarrow V_{vessel} = \frac{125\pi}{2} - \frac{625 \pi}{24} = \frac{875 \pi}{24} =114.5 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 4:

Volume generated by rotation about $y$

$$V_{rev} = \int_0^{2.5} 2\pi (x) \left( \frac{16}{25}x^3 \right) \ \mathrm{d}x = \frac{32\pi}{25} \left[ \frac{1}{5}x^5 \right]^{2.5}_0 = \frac{32 \pi}{125} \times 2.5^5 = 25 \pi$$ $$\Rightarrow V_{vessel} = \frac{125\pi}{2} - 25 \pi = \frac{75 \pi}{2} = 117.8 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Part 4: Level when half full

We can find the volume of revolution at some general height $h$, set this volume $V(h)$ to half the volume of the vessel and solve for $H$ the height at this volume.

Curve 1:

$$V(h) = \pi \int_0^h x^2 \ \mathrm{d}y$$ $$y = 4x \quad \Rightarrow \quad x = \frac{1}{4}y$$ $$ V(h) = \pi \int_0^h \frac{1}{16}y^2 \ \mathrm{d}y = \frac{\pi}{16} \left[ \frac{1}{3}y^3 \right] ^h_0 = \frac{\pi}{48} h^3$$

From above $V_{vessel} = \frac{125 \pi}{6}$

$$\Rightarrow \frac{\pi}{48} H^3 = \frac{1}{2} \frac{125 \pi}{6}$$ $$\Rightarrow H = = \sqrt[3]{48 \frac{125}{12}} = \sqrt[3]{500} = 7.937 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 2:

$$V(h) = \pi \int_0^h x^2 \ \mathrm{d}y$$ $$y = \frac{8}{5}x^2 \quad \Rightarrow \quad x = \left( \frac{5}{8}y \right)^{\frac{1}{2}}$$ $$V(h) = \pi \int_0^h \frac{5}{8}y \ \mathrm{d}y = \frac{5\pi}{8} \left[ \frac{1}{2}y^2 \right] ^h_0 = \frac{5\pi}{16} h^2$$

From above $V_{vessel} = \frac{125 \pi}{4}$

$$\Rightarrow \frac{5\pi}{16} H^3 = \frac{1}{2} \frac{125 \pi}{4}$$ $$\Rightarrow H = \sqrt{\frac{16}{5} \frac{125}{8}} = \sqrt{50} = 7.071 \mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 3:

In order to evaluate the volume by the method of discs I would first need to arrange the function into the form $x = f(y)$, this may be quite difficult. For this reason, we shall evaluate the volume using the method of shells.

The method of shells will not give the volume of the vessel directly; instead it gives the volume to the right of the curve rather than left. To find the volume of the vessel we must subtract the volume of revolution from the volume of a cylinder of radius $x$ and height $y$.

$$V(x) = \pi x^2 y - \int_0^x 2 \pi x y \ \mathrm{d}x$$

We need to get this equation in terms of one unknown $x$, we can eliminate $y$

$$y = \frac{24}{125}x^4 + x$$ $$V(x) = \pi x^2 \left( \frac{24}{125}x^4 + x \right) -2 \pi \int_0^x \frac{24}{125} x^5 + x^2 \ \mathrm{d}x = \pi \left( \frac{24}{125}x^6 + x^3 - 2 \left[\frac{4}{125}x^6 + \frac{1}{3}x^3 \right] ^x_0 \right) = \pi \left( \frac{16}{125}x^6 + \frac{1}{3}x^3 \right)$$

From above $V_{vessel} = \frac{875 \pi}{24}$, calling the radius of the vessel at the half full point $R$

$$\Rightarrow \pi \left( \frac{16}{125}R^6 + \frac{1}{3}R^3 \right) = \frac{1}{2} \frac{875 \pi}{24}$$ $$\Rightarrow \frac{16}{125}(R^3)^2 + \frac{1}{3}R^3 - \frac{875}{48} = 0$$

Quadratic in $R^3$, solving gives one positive solution:

$$R^3 = 10.703 \Rightarrow R = \sqrt[3]{10.703} = 2.204$$

Using equation of curve to find corresponding depth $H$:

$$H = \frac{24}{125}R^4 + R = 6.732\mathrm{\ cm^3 \quad (4\ s.f.)}$$

Curve 4:

$$V(h) = \pi \int_0^h x^2 \ \mathrm{d}y$$ $$y = \frac{16}{25}x^3 \quad \Rightarrow \quad x = \left( \frac{25}{16}y \right)^{\frac{1}{3}}$$ $$V(h) = \pi \int_0^h \left( \frac{25}{16}y \right)^\frac{2}{3} \ \mathrm{d}y = \frac{5\sqrt[3]{5}\pi}{4\sqrt[3]{4}} \left[ \frac{3}{5}y^\frac{5}{3} \right] ^h_0 = \frac{3\sqrt[3]{5}\pi}{4\sqrt[3]{4}} h^\frac{5}{3}$$

From above $V_{vessel} = \frac{75 \pi}{2}$

$$\Rightarrow \frac{3\sqrt[3]{5}\pi}{4\sqrt[3]{4}} H^\frac{5}{3} = \frac{1}{2} \frac{75 \pi}{2}$$ $$\Rightarrow H = \left( \frac{4\sqrt[3]{4}}{3\sqrt[3]{5}\pi} \frac{75}{4} \right)^\frac{3}{5} = \left( \frac{25\sqrt[3]{4}}{\sqrt[3]{5}} \right)^\frac{3}{5} = \sqrt[5]{12500} = 5\sqrt[5]{4} = 6.598\mathrm{\ cm^3 \quad (4\ s.f.)}$$