Immersion

Consider these solids:

1) A sphere of radius 1cm
2) A solid cylinder with height $\frac{4}{3}$cm and radius $1$cm
3) A solid circular cone with base radius $1$cm and height $4$cm.
4) A solid cylinder of height $\frac{4}{9}$cm with a hole drilled through it, leaving an annular (ring-shaped) cross-section with internal radius $1$cm and external radius $2$cm.

Can you sketch what each solid would look like?
Can you work out the volume of each solid?

Experiments are conducted where a solid is chosen and has a string firmly attached at a fixed point. The solid is then lowered at a rate of 1cm per minute into a beaker of water and the height of displaced water measured, with graphs of height against time drawn.

The results are measured on the following chart:


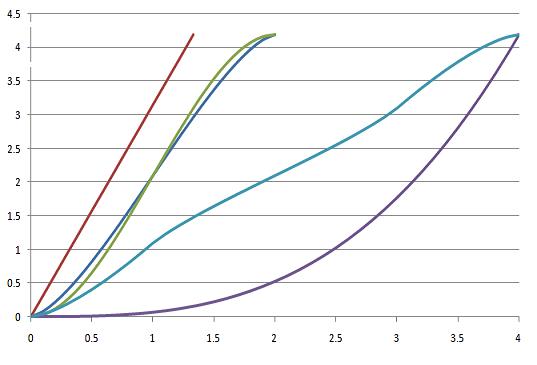
Can you work out what the two axes represent?

Can you work out which curve corresponds to which solid and in which orientation it is lowered into the beaker? (Note: One solid is used twice, in two different orientations).

Could you sketch the curve for the same solids in other orientations? What about different solids?

Extension task: Can you find equations which represent the volumes of the immersed parts of the solids? They vary in difficulty; if you cannot find the equation explicity, can you describe clearly what needs to be found? Reproduce as much of the above graph as you can.