Neural Nets

This problem will introduce you to the ideas behind neural networks. The tasks become more difficult as the problem progresses!

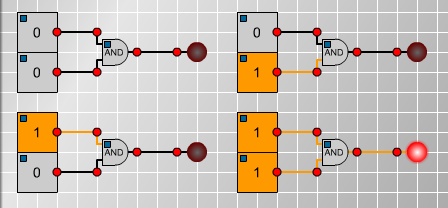
In standard mathematical logic, a logic gate activates, or 'fires' depending on whether certain inputs are either ON of OFF. Here's an example of an AND gate:

In the human brain, there are around $10^{11}$ neurons. Each of these is connected to many other neurons by synapses, the junctions between cells, which allow signals to be transmitted from cell to cell electrically or chemically. Each neuron has a resting potential (the value at which it remains unless stimulated) and a threshold potential (the value at which it will transmit a signal). Each input can carry potential differences; if the sum of the inputs raises the potential of the neuron to the threshold potential, the neuron fires.

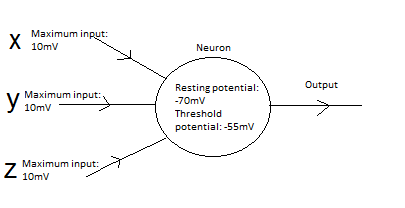
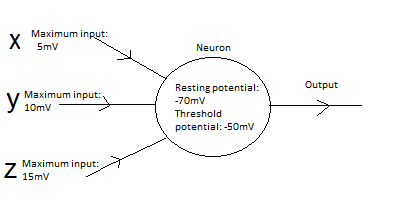
Imagine neurons with three inputs x, y, z. By treating x, y and z as coordinates in three dimensions, describe geometrically the regions for which the neurons fire in the follow pair of examples:

We can model the electrical circuits mathematically using?an artificial neural network. These contain input and output neurons, and also may contain hidden neurons. Each neuron has a threshold value $T$, and also a weight factor $W$, by which its output is amplified or deamplified. Here's an example of an OR gate. (The initial inputs are $0$ or $1$)

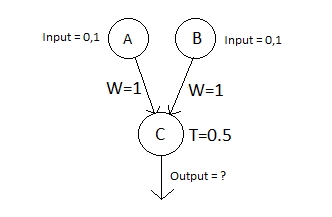
Verify that the output behaves as claimed. (i.e. C=1 if at least one of A or B is equal to 1)

Here's another network. Which logical operation does this represent?

?

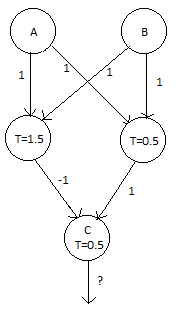
Can you create similar networks which replicate the behaviour of other logical operations?

So far, these are all examples of feed-forward circuits, i.e. the flow is all in one direction. We can also have feedback circuits, where the output of a neuron can feed back into the network at an earlier point. These can model the biological phenemenon of positive feedback, and the circuit can get extremely complicated very quickly. In more complicated applications we can consider the neuron as a function producing a numerical output from a vector of inputs.

Consider the following network in which the output feeds back into the input. Suppose that the output of the neuron is a function of the two input currents R and B. Suppose the the neuron system is initially charge free and then at some time a constant current of 1 is fired in A and an instantaneous pulse $P$ of current 1 is generated.


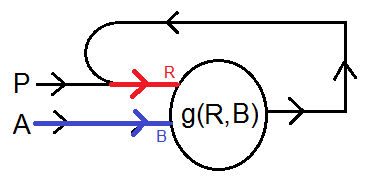
Consider the behaviour of the system in the case that $g(R,B)=\frac{1}{R+B}$ for different values of the initial pulse $P$.

Next consider the following similar system, which starts in a configuration with $A=C=1$ and $B=D=0$ and that $g(C, D)=C+D$ and $h(A,B) = 2^{-(A+B)}$ At the two junctions where the path splits into two, assume that half of the current flows down each. Where the two branches merge, the output is the sum of the two currents in the branches.


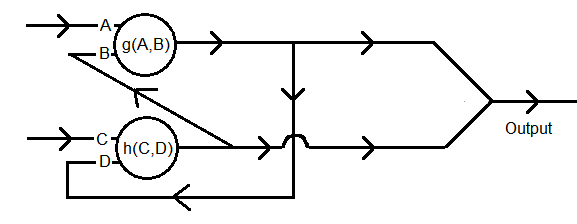
What is the output (to 6 decimal places)?

Suppose that the current in $C$ can be varied from $0$ to a large number. What range of outputs can be produced?

Suppose that $C$ and $A$ are initial pulses of current. Explore and explain your findings.

Explore for various functions $g$ and $h$.