Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Probably a Code?



- Problem
- Student Solutions
- Teachers' Resources
In fact, such a set of sequences occurring by chance is exceedingly unlikely (as determined experimentally) and thus points to structure in the code.
The text is the opening paragraph of Frankenstein, in which cqiog, hgzwp, jyqeo correspond to the strings "light", "ation", "which" etc.
You can see the encrypted text below:
We had three very nice solutions to this problem from Kirsten (Hornsey School for girls, England), Mookie Chau Lok Hang (Li Po Chun United World College of Hong Kong) and Maria (UK).
Mookie Chau even sent in a newly created code! We will include this on the site soon.
Kirsten said:
Reading through the problem, my initial thought was that Alice was right.
That many strings of 5(and more)or statistically quite unlikely and, in any
case, the letters are very unlikely to be "randomly generated
text". I did some more investigations to check- I found the
differences between the ends of the identical strings of letters.
My Results are
| Green | 35 |
| Red | 115 |
| Yellow | 795 |
| Dark green | 480 |
| Grey | 670 |
| Pink | 550 |
| Turquoise | 490 |
The noticable thing about these results is that they are all divisible by
5.
This adds strength to Alice's argument, making it less likely to be
coincidental.
I decided to try putting the letters into columns of 5. Though the
frequency analysis shows that it is not a letter for letter code, it could
be a polyalphabetic code (where more than one ciphers are used in
alternation).
I found the frequencies for the first column, made them into a graph and
matched it with the English frequencies. It was quite clear from the
patterns that it was a caesar shift, with plaintext a matching with cipher
text n. Feeling encouraged, I substituted that column and found the
frequencies for the others. After quite a long time trying to get my
computer to do what I wanted it to, I arrived at an answer which (mostly)
made sense. Filling in the word gaps gave the solution.
Kirsten continued to work out some probabilities:
I worked out the probability that ONE set of five
letters are the same for randomly generated letters of about 1600 letters:
Possible combinations: 26*26*26*26*26=11881376
Every digit could be one of 26 letters
I then used a spreadsheet to do the calculation
(11881376/11881376)*(11881375
/11881376) *(11881374/11881376)...to (11879781/11881376)
I did this to find out the probability that all the combinations
are different. The first has 11881376/11881376 that it will be different.
The second has 11881375/11881376
- everything except the first combination
This equals to 0.898407725, leaving a 0.101592275 chance that one
combination is the same. And thats just the chance that ONE pair is the
same.
Mookie Chau sent in these fascinating thoughts
Firstly, at first glance, it seems that the frequency looks random which is not encrypted by monoalphabetic substation cipher method. In order to prove my hypothesis, Index of Coincident (IC) is calculated which is 0.044. Since the value is closer to the IC of Polyalphabetic substitution cipher method (0.038), it suggests that the plaintext is probably encrypted by Vigenere (one kind of periodic substation cipher). The IC value is calculated by a program online which you can find it from http://www.caconsultant.com/maths/ under frequency analysis.
Before identifying the keyword used to encrypt the text, the length of the keyword should be found. It can be done by look for the sequences of letters that appear more than once in the ciphertext. The most likely is that the same sequence of letters in the plaintext has been enciphered using the same part of the key. Below is the list of sequences which appear more than once and their spacing between 2 of them is identified.
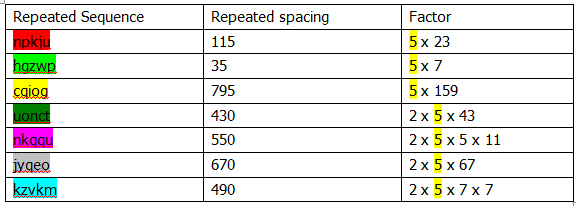
By finding their common factor which is 5, this probably suggests that the key only contains 5 letters.
We proceed as follows. We know that one of the rows of the Vigenere square, defined by L1, provided the cipher alphabet to encrypt the 1st, 6th, 11th, 16th, ”¦ letters of the message. Hence we should be able to use old fashioned frequency analysis to work out the cipher alphabet in question. Below is the frequency analysis of different columns (i.e. different letters):


By using simple substitution cipher method to decode it (for example, the highest frequency of letters are “e”, “t” and “a”), the key of the Vigenere can be found which is NRICH in this case.
Finally, using the program of the wesbite http://www.caconsultant.com/maths/, the whole plaintext can be recreated. In this example the plaintext is extracted from Frankenstein, Letter 1 written by Mary Shelley.
Maria from the UK writes:
Comparing the frequency of letters in the English language with the frequency of letters in the coded text, there is hardly any resemblance. In fact, most of the letters in the coded text have similar frequencies. This indicates that there is more than just a simple substitution cipher. From solving another Nrich cipher problem, I recognised that this was typical of a Vigenere cipher. However, there are ways we can check this assumption, as explained below.
Frequency in coded text
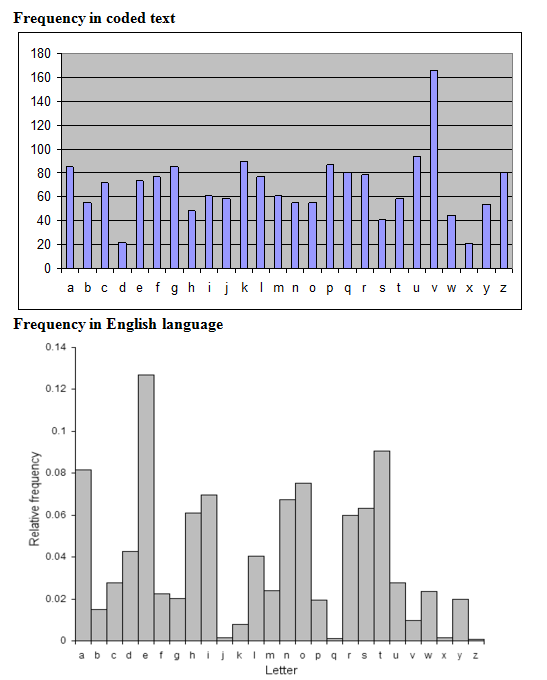
Frequency in English language
Let us first consider the strings of 5 repeated characters: How likely are we to find a repeated string of 5 letters in a random jumble? Given a string of 5 letters which are not necessarily distinct, there are $26^5$ possible permutations (each letter can be one of 26 letters). So given 2 random strings of 5 letters there is a 1 in 11 881 376 chance that they are the same. Since we have 1776
characters in the code, we have $1776-4=1772$ strings of 5 letters. The chance of 2 being the same is:
$$_{1772}C_{2}\times \frac{1}{11881376} = 0.132064333 \dots \approx \frac{1}{8}$$
(this is the number of pairings multiplied by the probability of 2 being the same). So the probability of this happening 7 times in the same set of 1776 characters is approximately $\frac{1}{8^7}$, or about 1 in 2 million. In other words, it would appear that the code we have been given is almost certainly not random, and these 5 letter strings are significant.
To investigate them further, we count the number of character between each of the 7 5-letter repeats, finding:
| 5 letters | Characters between 1st letters of each repeat |
| hpkju | 115 |
| cqiog | 795 |
| hgzwp | 35 |
| jyqeo | 670 |
| nkqqu | 550 |
| uonct | 430 |
| kzvkm | 490 |
We notice that all these numbers are multiples of 5: indeed, 5 is the only common factor of all 7 numbers. Hence we can deduce that if this is a Vigenere cipher, we are looking for a 5 letter codeword. The fact that all the numbers are multiples of 5 also backs up our assumption that we have a Vigenere cipher.
Analysing the frequency of every 5 letters, starting with the first letter, we see a pattern, which matches up well to the frequency of letters in the English language if we set with N in the code to A, O to B, P to C, etc. So the first letter of our codeword is N.
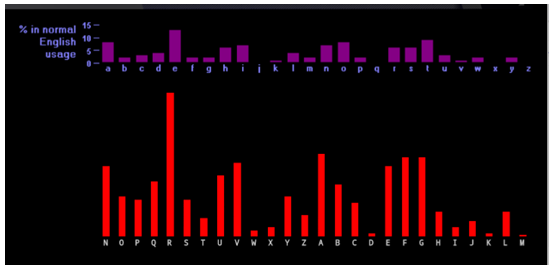
Continuing in this way with the other 4 sets of letters, we discover, (perhaps unsurprisingly!) that the codeword for this Vigenere cipher is NRICH. We end up with the text:
IAMALREADYFARNORTHOFLONDONANDASIWALKINTHESTREETSOFPETERSBURGH”¦
We can easily add spaces to this, obtaining:
I am already far North of London, and as I walk in the streets of Petersburg”¦
A quick Google of this passage, and we discover that the text encrypted is a paragraph of Letter 1 from Frankenstein by Mary Shelley. =)
You may also like
Game of PIG - Sixes
Can you beat Piggy in this simple dice game? Can you figure out Piggy's strategy, and is there a better one?
The Mean Game
Edward Wallace based his A Level Statistics Project on The Mean Game. Each picks 2 numbers. The winner is the player who picks a number closest to the mean of all the numbers picked.

