Advanced Scientific Mathematics

Age 16 to 18

Challenge Level Yellow star

stemNRICH : Science, Technology, Engineering, Mathematics enriched

Welcome to the Advanced Scientific Mathematics section of stemNRICH . This contains a set of activities designed to develop the advanced applied mathematical skills needed to make the most of the study of the physical sciences or engineering at university. These problems naturally follow on from the more elementary core scientific mathematics section of stemNRICH and are primarily intended for those who intend to study physics, engineering or applied mathematics at university.

Area of maths	Style	Question	Description
Rates of change		Maths Filler 2	Practise looking at rates of change as this vessel fills with water.
		Immersion	Various solids are lowered into a beaker of water. How does the water level rise in each case?
		Brimful	Rotate the curves to make some mathematical vessels.
		Brimful 2	Which of these mathematical flasks will eventually fill up with water?
Curves		Curve Fitter	Use your skill to try to fit a cubic equation through these three points.
		Curve Fitter 2	Can you make a cubic which has a certain distance between the turning points?
		Implicitly	Can you find the shape of this implicity defined function?
		Whose line graph is it anyway?	Which line graphs, processes and equations go together?
		Scientific Curves	Can you sketch these difficult curves, which have uses in mathematical modelling?
Calculus	Calculus is involved in many problems on stemNRICH. See the physNRICH and engNRICH pages for various particular examples.
		Calculus Countdown	Can you hit the target functions using a set of input function and a little calculus and algebra?
		Integration Matcher	Which curves, integrals and differentials go together?
		Operating Machines	What functions can you make using the function machines RECIPROCAL and PRODUCT and the operator machines DIFF and INT?
Differential equations	You will also find lots of differential equations problems in various sections on the physNRICH and engNRICH pages
		Differential Equation Matcher	Match the descriptions of physical processes to these differential equations.
		Reaction Rates	Explore the possible mathematical solutions to the non-linear order of reaction equation from chemistry.
Series and expansions		Production Equation	Each week a company produces X units and sells p per cent of its stock. How should the company plan its warehouse space?
		Stirling Work	See how enormously large quantities can cancel out to give a good approximation to the factorial function.
		What Do Functions Do for Tiny x?	How do these familiar functions behave for very small values?
		Bessel's Equation	Get further into power series using the fascinating Bessel's equation.
Powers, roots and logarithms	See also the Logarithms and pH problems on the chemNRICH pages
		Power Match	Can you locate these values on this interactive logarithmic scale?
		Debt Race	Who will be the first investor to pay off their debt?
Probability and distributions		pdf Matcher	What scientific stories can you match to these pdf curves?
		Circle PDF	How can an arc of a circle be a pdf?
		Scale Invariance	By exploring the concept of scale invariance, find the probability that a random piece of real-world data begins with a 1.
		Into the Exponential Distribution	Get into the exponential distribution through an exploration of its pdf.
		Into the Normal Distribution	Get into the normal distribution through an exploration of its pdf.
Statistics		Stats Statements	This question gives you 10 statistical statements. Develop your statistical intuition by asking yourself are they sometimes, always, nearly always, almost never or never true?'
		Overbooking	Why do airlines overbook?
		The Wrong Stats	Why MUST these statistical statements be at least a little bit wrong?
		Aim High	How much wheat should this farmer plant to minimise his expected loss?
		Time to Evolve 2	How would you model the time between your birth and that of your grandfather?
Trigonometry		Flight Path	Use simple trigonometry to calculate the distance along the flight path from London to Sydney.
		Loch Ness	Draw graphs of the sine and modulus functions and explain the humps.
		Spherical Triangles on Very Big Spheres	Find out about spherical triangles and decide if telecoms engineers need to know about such things.
		Taking Trigonometry Seriesly	Look at the advanced way of viewing sin and cos through their power series.
Complex numbers		An Introduction to Complex Numbers	A nice introduction to complex numbers, including many exercises for the reader.
Complex numbers		More on the way	More on the way
Vectors		Spotting the Loophole	A visualisation problem in which you search for vectors which sum to zero from a jumble of arrows. Will your eyes be quicker than algebra?
		Vector Walk	Starting with two basic vector steps, which destinations can you reach on a vector walk?
		Polygon Walk	Follow Ulaf, Vicky and Wilber on a vector walk to determine the locations nearest to the origin.
		Air Routes	An application of vectors and scalar products in a very practical setting.
		Cross with the Scalar Product	Explore the meaning of the scalar and vector products and see how the two are related
Vectors and matrices		Square Pair	What quadrilaterals can you transform this pair of squares into?
		Transformations for 10	Explore the mathematics of matrix transformations with these 10 individual questions.
		Matrix Meaning	Explore the algebraic and geometric properties of matrices with these 5 individual questions.
		Crystal Symmetry	Use vectors and matrices to explore the symmetry properties of Caesium Chloride.
		Nine Eigen	Explore how matrices can fix vectors and vector directions.?
		Fix Me or Crush Me	Can you make matrices which will fix one lucky vector and crush another to zero?
Numerical methods		Root Hunter	In this short problem, try to find the location of the roots of some unusual functions by finding where they change sign.

		Building Approximations for Sin(x)	Build up the concept of the Taylor series.
Decision making and algorithms		Testing Strategy	Investigate ways in which you could implement a scoring system for a multiple choice test.
Decision making and algorithms	.	.	.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Advanced Scientific Mathematics

You may also like

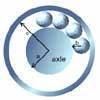
Ball Bearings

Overarch 2

Cushion Ball