Skip over navigation
Folding Fractions
Age 14 to 16
Challenge Level 
Why do this problem?
This problem investigates in more detail the relationships found in Folding Squares.
Relationships can be discovered by making accurate paper folds or diagrams, but there is also scope for some sophisticated geometrical reasoning, manipulation of fractions and finding and justifying general rules for the different fractions that can be made.Possible approach
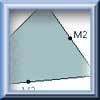
Learners could start by marking off quarters along one side of a square, and making folds from the corner to these marks, as shown in the diagrams. Pose the question "What fraction of the diagonal do you think is formed by the line joining to a quarter of the way along the side? Half way? Three quarters?"
Learners can measure the lengths of the lines on their diagram to see if their conjectures appear to be right - they may be surprised by the results.
Once they have built up a picture of what is happening with quarters, they can investigate what happens when the side is divided into eighths. As it is not always easy to measure accurately enough and the fractions are not always obvious, learners might think about how to work more systematically and/or decide to use a more analytical approach. Moving them towards more formal and less
experimental methods could be encouraged through discussion and sharing of ideas.
Groups may wish to present their findings through posters.
Key questions
How can you organise your work so that you are able to identify any patterns that emerge?
How can you be sure of the fractions that appear to be emerging when you measure?
What mathematics have you met before that might be useful here?
What do you think would happen if we divided the side into fifths? Sixths?
Possible extension
If I divided the side of my square into $n$ equal portions, what fraction of the diagonal would I get by folding to $\frac{m}{n}$ of the way along the side?
What other quadrilaterials will this idea apply to and does the rule need modification in any particular cases?
Possible support
Start with Folding Squares and build up ideas about halves and quarters before trying to generalise.You may also like
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Pareq Exists
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines.
The Medieval Octagon
Medieval stonemasons used a method to construct octagons using ruler and compasses... Is the octagon regular? Proof please.