Back Fitter
Several experiments were performed and data measured over a period of 10 hours.
The resulting charts are shown below.
Can you find algebraic equations which closely match the curves, which could be used to predict values of the variables at other times? There might be many possible curves of the right sort of shape by eye, so a numerical plot will be needed to discover the most likely candidates.
The following Office 2003 spreadsheet will allow you easily to compare plots of the likely curves against the actual data - the intention is that you will tackle this problem numerically.
Note: The different sets of experimental data are distinct, so try as many or as few as you like. Fitting all of the sets will present quite a challenge!
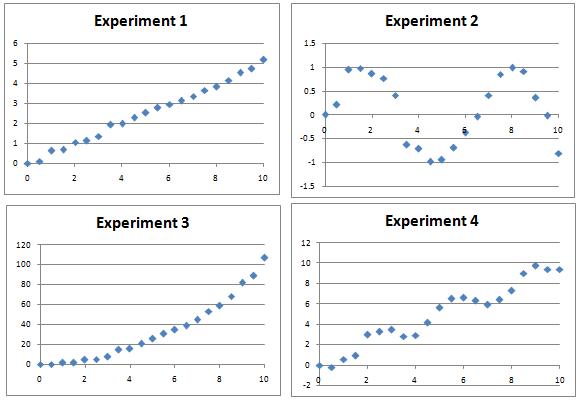
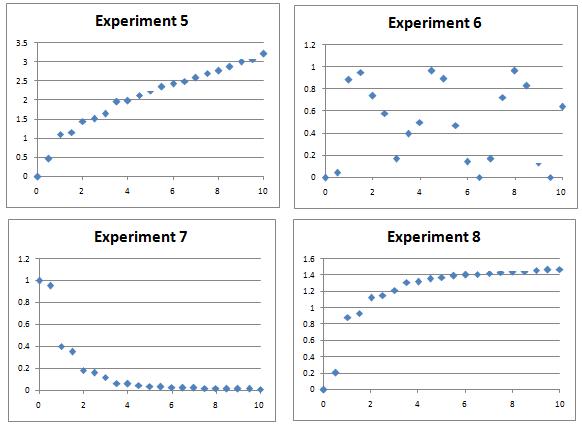
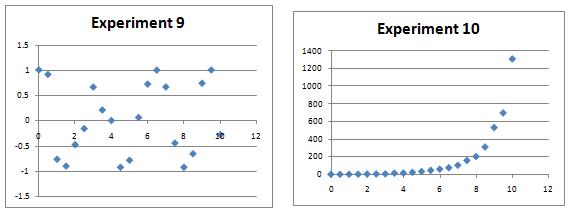
Extension: Whilst there are 'obvious' candidates for each data set, can you find multiple functions which give rise to apparently good matches to some of the data sets? How might you numerically determine which fits are best?
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Archimedes and Numerical Roots
The problem is how did Archimedes calculate the lengths of the sides of the polygons which needed him to be able to calculate square roots?