Skip over navigation
I made this into a formula.
If the original line is $y=ax+b$, and we move $X$ right and $Y$ up, then the new line is $y=ax+b-aX+Y$. So the constant becomes $b-aX+Y$.
So the constant is the same, but minus the gradient times the movement (if you move left then $X$ is negative), and then plus the vertical movement (of you move down then $Y$ is negative).
So the pairs are:
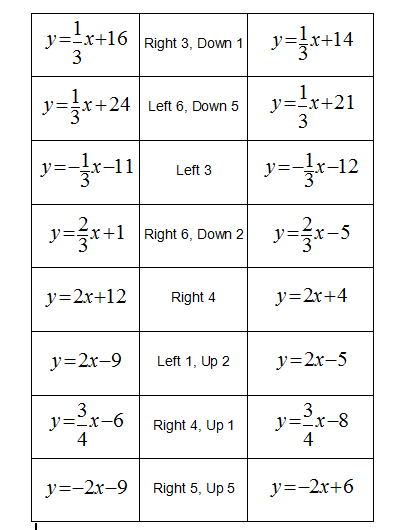
So lots of values of $X$ and $Y$ will make these work, as you can make equations that describe the motion, and then any solutions will work. You could even plot the solutions, they themselves would be straight line graphs.
So for $y=2x+1$ translated to $y=2x-4$, the $X$ and $Y$ motion satisfies $1-2X+Y=-4$ by the equation above, so any $X,Y$ satisfying $Y-2X=-5$ will do the translation above.
Translating Lines
Age 11 to 14
Challenge Level 
Jiwon Jung noticed:
You can tell it's translated because the gradient hasn't changed, and the pairs of lines are parallel.
Ellie from Chiswick expanded and gave reasoning;
I experiemented with the lines and translations. I noticed
that if you just translate up and down (in the $y$ direction) then
the constant goes up or down the same number of places as the left
has moved.
If you move sideways, then it is in proportion to the gradient
of the line.
I made this into a formula.
If the original line is $y=ax+b$, and we move $X$ right and $Y$ up, then the new line is $y=ax+b-aX+Y$. So the constant becomes $b-aX+Y$.
So the constant is the same, but minus the gradient times the movement (if you move left then $X$ is negative), and then plus the vertical movement (of you move down then $Y$ is negative).
So the pairs are:
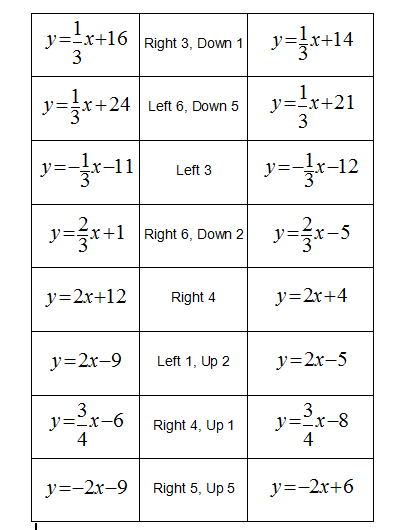
So lots of values of $X$ and $Y$ will make these work, as you can make equations that describe the motion, and then any solutions will work. You could even plot the solutions, they themselves would be straight line graphs.
So for $y=2x+1$ translated to $y=2x-4$, the $X$ and $Y$ motion satisfies $1-2X+Y=-4$ by the equation above, so any $X,Y$ satisfying $Y-2X=-5$ will do the translation above.
Related Collections
You may also like
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?
Khun Phaen Escapes to Freedom
Slide the pieces to move Khun Phaen past all the guards into the position on the right from which he can escape to freedom.
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.