Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Surprising Transformations



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Freida from Little Chalfont Primary School and Richard from Wilson's School found one way of starting at $y = 4x + 7$ and ending at $y = 4x-2$:
Translate down by three units,
Translate left by two units.
Sophie, Evie and Sinthu from Dr Challoner's
High School also started with the same two reflections but then
switched the translations and still ended at $y = 4x-2$:
Translate left by two units,
Translate down by three units.
Keira, Christina and Amy, also from Dr
Challoner's High School, explained why they also started with a
pair of reflections:
Translate left by two units,
Translate down by three units.
We discovered that when you do it in this order the gradient is either 4 or -4. Knowing this we put the reflections next to each other as it means that the gradient goes from 4 to -4 and back to 4.
4 is the gradient of the line we want to end up with so it's just a matter after that of putting the translations on the end, and the order of both translations doesn't matter as they result in the same line.
Some students found more than one way of reaching $y = 4x-2$.
Amanda and Kat from Dr Challoner's High School wrote:
We think there are 4 solutions to the question.
Solution 1:
Reflect in the horizontal axis,
Reflect in the vertical axis,
Translate down by 3 units,
Translate left by 2 units.
Solution 2:
Reflect in the horizontal axis,
Reflect in the vertical axis,
Translate left by 2 units,
Translate down by 3 units.
Solution 3:
Reflect in the vertical axis,
Reflect in the horizontal axis,
Translate left by 2 units,
Translate down by 3 units.
Solution 4:
Reflect in the vertical axis,
Reflect in the horizontal axis,
Translate down by 3 units,
Translate left by 2 units.
In conclusion, to get the same outcome each time, you must reflect in the vertical and horizontal axes first, no matter what order you do it in, as long as you do them first, one after the other, so that the line will always end in the same place ($y = 4x-7$) after those 2 reflections. Then you can do either of the translations in any order, because it will always end up in the same place ($y = 4x-2$), as long as you've done the reflections first.
Jack from Hertford South Primary drew a table of all the
possibilities and explains:
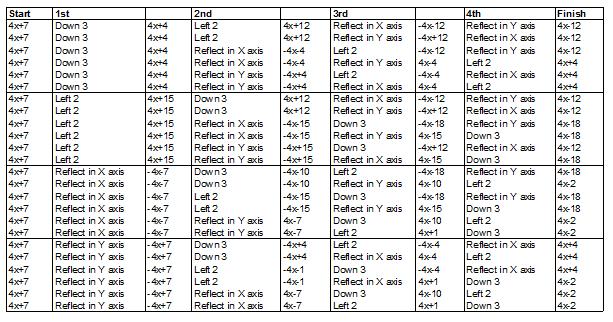
So there are 24 orders of 4 transformations, and only 4 possible finishing graphs. There are 6 ways to make $y=4x-12$, 6 ways to make $y=4x+4$, 6 ways to make $y=4x-18$ and 6 ways to make what we were looking for $y=4x-2$.
You may also like
A Problem of Time
Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?
Tricircle
The centre of the larger circle is at the midpoint of one side of an equilateral triangle and the circle touches the other two sides of the triangle. A smaller circle touches the larger circle and two sides of the triangle. If the small circle has radius 1 unit find the radius of the larger circle.
Attractive Tablecloths
Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?

