Skip over navigation
Classical Means
Age 16 to 18
Challenge Level 
|
Why do this
problem?
 |
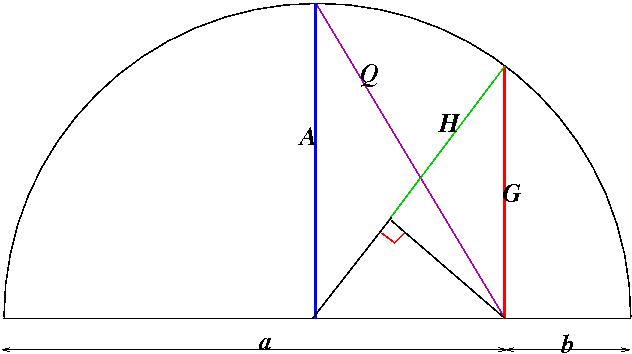Doing this problem you need to visualise the relationship between the formulae for the arithmetic, geometric and harmonic means in terms of the radius of a circle and the geometry of similar triangles and Pythagoras Theorem. This process involves a beautiful blend of algebra and geometry. It provides a good exercise for learners in mathematical reasoning and proof. The mathematical concepts are simple and the interplay of ideas to give the necessary proofs is good experience for learners. |
Possible approach
Ask the learners to work out the radius of the semicircle in
terms of $a$ and $b$. Then ask them to identify all the triangles
and to discuss with a partner, and write down, everything they
observe about the triangles. They may then be able to do the
problem for themselves. If not the following questions should
provide some assistance.
Key questions
Can you find the radius of the semicircle?
Can you see a right-angled triangle with $G$ as the length of
one side and use this to find $G$ in terms of $a$ and $b$?
Can you use similar triangles to find a relationship between
$A$, $G$ and $H$?
Can you use similar triangles to find a formula for $H$ in
terms of $a$ and $b$?
Can you you use the geometry of triangles to compare the
lengths of $A$, $G$ and $H$?
Can you see a right-angled triangle with $Q$ as the length of
one side and use this to find $Q$ in terms of $a$ and $b$?
Possible
extension
Try the problem
Pythagorean Golden Means and read the article
About Pythagorean Golden Means
Possible support
Try the problem
Harmonic Triangle.
You may also like
Shades of Fermat's Last Theorem
The familiar Pythagorean 3-4-5 triple gives one solution to (x-1)^n + x^n = (x+1)^n so what about other solutions for x an integer and n= 2, 3, 4 or 5?
Code to Zero
Find all 3 digit numbers such that by adding the first digit, the square of the second and the cube of the third you get the original number, for example 1 + 3^2 + 5^3 = 135.