Ramping it Up

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

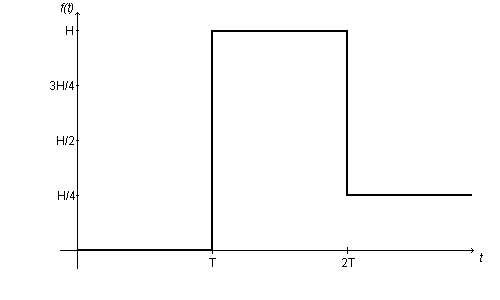
At a time T, a car mounts a curb of height $H$, and its front suspension undergoes a sudden change. At a time 2T, the car drops down the other side of the curb to $\frac{1}{4}H$. It is suggested that the graph of this process is as given as a function $f(t)$ above.

Try to work out the graph of $f$ '$(t)$ against $t$. What parts make sense and what parts don't? Could you alter the graph of $f(t)$ slightly to make the derivative function make more sense?

Next imagine that a car drives at a steady $20$ km h$^{-1}$ over a concrete block of height $10$cm and rectangular cross section of width $50$ cm. Make a mathematical model of the height of the front suspension over time. Be clear as to your assumptions and make a clear note of any possible refinements to your model.

What does your model say about the derivative of the height over time?

What is the maximum G-force the suspension of a car is likely to be subjected to in normal use?

On a physical note, think about the implications that this sort of modelling process might have on the design of shock-absorbers for cars.