Pack Man
Atoms can be thought of as hard spheres of a fixed radius, for many purposes in physics.
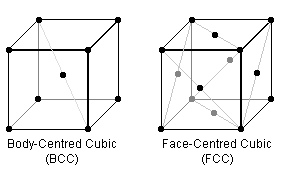
In the BCC & FCC crystal lattice arrangements (the repeating cube of each is pictured above), certain planes are "close packed" i.e. the "hard spheres" are thought of as touching. Steels can have either packing structure, but are generally structurally better in the more densely-packed form which, for example, don't become brittle at low temperatures.
To begin, visualise the crystal arrangements above where the black dots represent the centre of identical spherical atoms of fixed radii which just touch each other.
Can you tell which of BCC or FCC is this better, more dense form? Can you prove it?
Pure copper is structured in the FCC form, has atomic mass 63.5, and atomic radius 128 picometres. Estimate the density of copper. How does your result compare with the actual density of copper?
You may also like
2D-3D
Two circles of equal size intersect and the centre of each circle is on the circumference of the other. What is the area of the intersection? Now imagine that the diagram represents two spheres of equal volume with the centre of each sphere on the surface of the other. What is the volume of intersection?
The Dodecahedron Explained
What is the shortest distance through the middle of a dodecahedron between the centres of two opposite faces?
When the Angles of a Triangle Don't Add up to 180 Degrees
This article outlines the underlying axioms of spherical geometry giving a simple proof that the sum of the angles of a triangle on the surface of a unit sphere is equal to pi plus the area of the triangle.