Skip over navigation
Symmetric Angles
Age 14 to 16
ShortChallenge Level 
The diagram has rotational symmetry of order four about D.
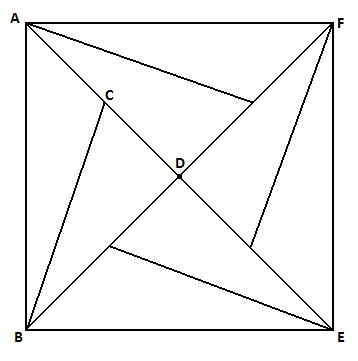
If angle ABC is 15^{\circ} and the area of ABEF is 24cm^2, what is the length of CD?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Compare Areas
Which has the greatest area, a circle or a square, inscribed in an isosceles right angle triangle?
Take a Square
Cut off three right angled isosceles triangles to produce a pentagon. With two lines, cut the pentagon into three parts which can be rearranged into another square.
Semi-detached
A square of area 40 square cms is inscribed in a semicircle. Find the area of the square that could be inscribed in a circle of the same radius.