Skip over navigation


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Symmetric Angles
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
As the figure has rotational symmetry of order $4$, $ABEF$ is a square.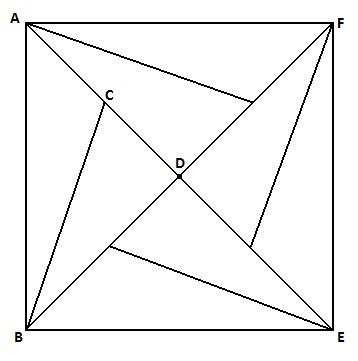
Area $ABEF=4\times$area$\triangle BDA=4\times \frac{1}{2}BD \times DA=2(DB)^2=24$cm$^2$, so $BD=\sqrt{12}$cm$=2\sqrt{3}$cm.
As $ABEF$ is a square, $\angle ABD=45^{\circ}$ so $\angle CBD=45^{\circ} -15^{\circ} =30^{\circ}$.
Since $\tan {30^{\circ}}= \frac{CD}{BD}=\frac{CD}{2\sqrt{3}}$, we have $CD=2\sqrt{3}\tan{30^{\circ}}$cm.
Now consider the following equilateral triangle with side lengths $2$:
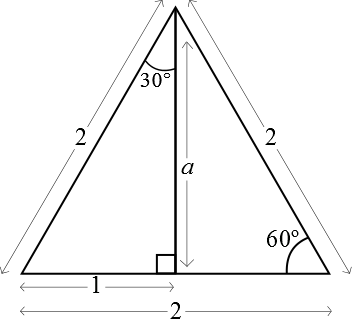
The vertical line is perpendicular to the base-line and so bisects both the angle at the top vertex and the base-line.
Consider the left right-angled triangle. Pythagoras' theorem gives $a=\sqrt{3}$ and then we have $\tan{30^{\circ}}=\frac{1}{a}=\frac{1}{\sqrt{3}}$
Therefore $CD=2\sqrt{3}\tan{30^{\circ}}$cm$=2$cm.

Area $ABEF=4\times$area$\triangle BDA=4\times \frac{1}{2}BD \times DA=2(DB)^2=24$cm$^2$, so $BD=\sqrt{12}$cm$=2\sqrt{3}$cm.
As $ABEF$ is a square, $\angle ABD=45^{\circ}$ so $\angle CBD=45^{\circ} -15^{\circ} =30^{\circ}$.
Since $\tan {30^{\circ}}= \frac{CD}{BD}=\frac{CD}{2\sqrt{3}}$, we have $CD=2\sqrt{3}\tan{30^{\circ}}$cm.
Now consider the following equilateral triangle with side lengths $2$:

The vertical line is perpendicular to the base-line and so bisects both the angle at the top vertex and the base-line.
Consider the left right-angled triangle. Pythagoras' theorem gives $a=\sqrt{3}$ and then we have $\tan{30^{\circ}}=\frac{1}{a}=\frac{1}{\sqrt{3}}$
Therefore $CD=2\sqrt{3}\tan{30^{\circ}}$cm$=2$cm.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Compare Areas
Which has the greatest area, a circle or a square, inscribed in an isosceles right angle triangle?
Take a Square
Cut off three right angled isosceles triangles to produce a pentagon. With two lines, cut the pentagon into three parts which can be rearranged into another square.
Semi-detached
A square of area 40 square cms is inscribed in a semicircle. Find the area of the square that could be inscribed in a circle of the same radius.

