Skip over navigation
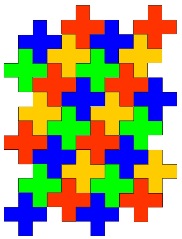
I used $28$ tessellating crosses, which are on the file. Looks quite cool. The scary thing is, after copying and pasting $28$ crosses (having just made them a random size), I, co-incidentally, couldn't fit any more than $28$ on the page ...
I got grid paper and drew $14$ squares that were touching and drew a line diagonally through every square. I got $28$ triangles because I had $14$ squares and split them in $2$ which made $28$ because $14+14=28$. That is how I got $28$ triangles.
So It's 28
Age 5 to 7
Challenge Level 
We had very few ideas sent in but it seems that most pupils went on to the other challenge focussed on $28$: $28$ and It's Onwards and Upwards.
Matthew wrote the following and sent in the picture to go with it:
I used $28$ tessellating crosses, which are on the file. Looks quite cool. The scary thing is, after copying and pasting $28$ crosses (having just made them a random size), I, co-incidentally, couldn't fit any more than $28$ on the page ...
and Emma wrote:
I got grid paper and drew $14$ squares that were touching and drew a line diagonally through every square. I got $28$ triangles because I had $14$ squares and split them in $2$ which made $28$ because $14+14=28$. That is how I got $28$ triangles.
You may also like
Homes
Six new homes are being built! They can be detached, semi-detached or terraced houses. How many different combinations of these can you find?
Number Squares
Start with four numbers at the corners of a square and put the total of two corners in the middle of that side. Keep going... Can you estimate what the size of the last four numbers will be?
Stairs
This challenge is to design different step arrangements, which must go along a distance of 6 on the steps and must end up at 6 high.