28 - Upward and Onward

28 - Upward and Onward

You may like to have a go at the problem So It's 28 before trying this challenge.

 

 

We are about to explore the number 28.

In 2010 the month of February had four weeks of 7 days making 28 days altogether.

 

----------

 

Half a pack of cards with the jokers makes 28 cards altogether:

 

 

----------

The seventh triangular number is also 28:

 

 

But all these examples of 28 are just flat - or you might call them 2D.

 

I'm suggesting we try making something 3D.

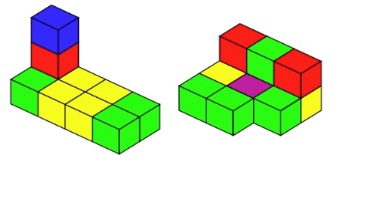
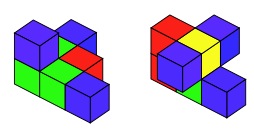
How about if we put some small cubes together and count the faces which are visible. Can we arrange the cubes so that there are exactly 28 faces?

In the pictures above, we're not counting faces that are 'on the table'. I've coloured the cubes (according to how many faces are showing) to make the counting a little easier.

 

 

It would probably be good to make one of these shapes and do your own counting.

Can you arrange some cubes so that 28 of their faces are visible?

 

----------

 

You might want to try another way with a new shape resting on a glass table (you could just pretend!) so you can count the faces underneath too. Here are two shapes:

Cubes that click together might make it easier.

----------

 

So this is your challenge: make a shape that has 28 little square faces visible.

Now try on a pretend glass table and see how many you can make then. Any surprises?

You may like to take photos of them.

Please send in any thoughts, ideas or pictures relating to your explorations.

Why do this problem?

Possible approach

You could introduce this activity by sharing the examples of 28 in the problem and asking if any of them know something special about the number 28.

Show the group an arrangement of cubes resting on a surface and explain that 28 small faces are visible. Check that everyone is happy that we're not counting the faces that are resting on the surface. Encourage learners to work in pairs to find other arrangements which have 28 faces. Depending on your supplies of cubes, you can suggest children keep each arrangement once it is made, or that they record it in some way. (Isometric paper may be useful.)

You may like to keep this challenge as an ongoing 'simmering' activity which children add to over a period of a number of days/weeks.

Key questions

Tell me about this.
Have you anything to say about this shape that you have made?`
How could you change your shape and still have 28 faces showing?

Possible extension

Children could explore other notable things about 28, for example it's a hexagonal number. 28 is the sum of the first five consecutive primes: 2, 3, 5, 7, 11. You might like to introduce them to perfect numbers.

Possible support

Plenty of cubes will be needed for this activity. If children are struggling to record their arrangements, digital photographs may be the answer.