28 - Upward and Onward

We had some lovely ideas sent in. It would have been good to be there when they were created and to know how you got your solutions. Here are just a few. I was interested in both Alexander's and George's good descriptions in words to say what they created.

Alexander wrote:

I used $9$ bricks. I put $8$ of them together in a $3$ by $3$ square with the middle one missing. I then put the $9$th brick on the middle brick of one of the rows. So I had one brick with $5$ faces showing, $7$ bricks with $3$ faces showing and $1$ brick with $2$ faces showing.

and George wrote;

I used $11$ bricks. I had $1$ row of $3$ bricks joined to a row of $4$ bricks and the $4$ brick row was joined to another row of $3$ bricks. On one of the rows of $3$ bricks I put the $11$th brick at the end on top.

Ewan, Fraser, Jenny Lee and Ayan had a good idea of only counting the faces you could see, so they sent in this picture;

Kristy and Amy used the computer and sent in;

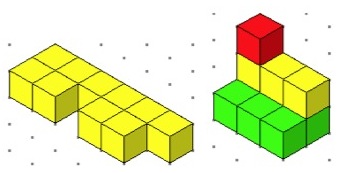
Zain sent in two ideas, one of which is;

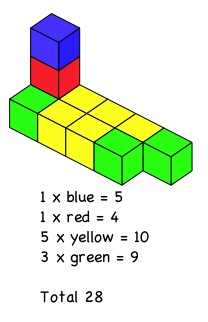
Finally Lily and Alex sent in:

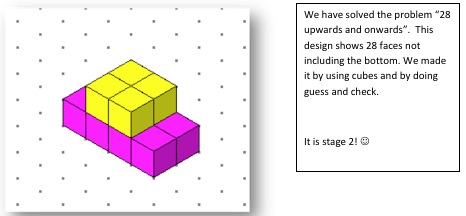
Well done everyone! I'm sure that many more of you who did not send in solutions came up with some interesting ideas and if your class/group did not have a go try it now!