Skip over navigation
Preveina from Crest Girls' Academy made a start on this problem:
For three points, there are always infinitely many such triangles because every time you extend the length of the lines in a triangle you will be making a new point; by doing this you'll be producing unique triangles every time. This then leads on having infinity triangles made.
The picture below shows a sequence of triangles - the black lines pass through two of the points, and a variety of lines can pass through the third point, extending one of the lines in the original triangle.
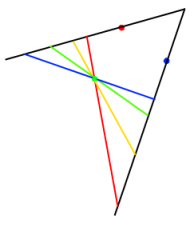
Preveina went on to show some examples of configurations of four and five points where a triangle could be drawn.
To consider whether all configurations are possible, consider the set of points below:
Can you find a way to draw a triangle passing through all four points? Can you convince yourself it is impossible?
Close to Triangular
Age 14 to 16
Challenge Level 
Preveina from Crest Girls' Academy made a start on this problem:
For three points, there are always infinitely many such triangles because every time you extend the length of the lines in a triangle you will be making a new point; by doing this you'll be producing unique triangles every time. This then leads on having infinity triangles made.
The picture below shows a sequence of triangles - the black lines pass through two of the points, and a variety of lines can pass through the third point, extending one of the lines in the original triangle.
Preveina went on to show some examples of configurations of four and five points where a triangle could be drawn.
To consider whether all configurations are possible, consider the set of points below:
Can you find a way to draw a triangle passing through all four points? Can you convince yourself it is impossible?