The Numbers Give the Design

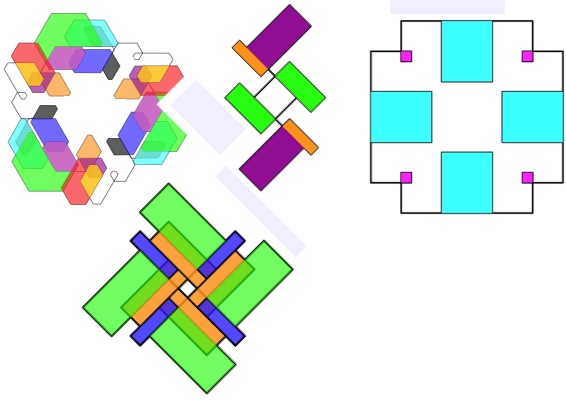
How about making designs like the ones above?

It's just a matter of getting a group of numbers together that repeat and then using a simple drawing rule, then colouring the pattern in.

A good way to start is to take a number sequence that you like, for example square numbers or the $3$ times table.
Just keep the ones (units) of those numbers, for example $1, 4, 9, 6, 5, 6, 9, 4, 1, 0, 1, 4$ etc. or $3, 6, 9, 2, 5, 8, 1, 4, 7, 0, 3, 6$ etc.
You may notice that with these, and perhaps your own sequences, they go to a $0$ and then repeat.

For this challenge, you just need the numbers that go as far as just before the zero, for example $1, 4, 9, 6, 5, 6, 4, 1$ or $3, 6, 9, 2, 5, 8, 1, 4, 7$.

Now to draw ...

Using squared paper and starting somewhere in the middle, take each of the numbers in turn to tell you how long to draw the line and turn a right angle to the left after you've drawn each line.

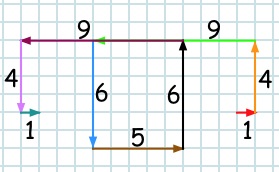
This may help you to see what to do, using the example of square numbers and starting with the red $1$. I've coloured each new line with a different colour:

After the final $1$ you start again as shown below:

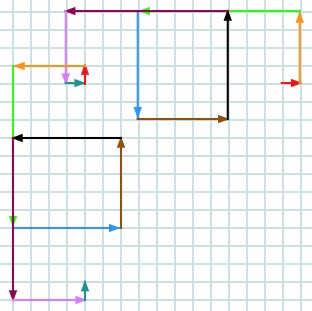
and so on until you get back to the beginning.
Some squences that you choose may not come back to the start but just keep stepping away!

So now it's your turn ...
Choose your sequence.
Pick out the ones (units) until you find it repeating.
Draw the lines carefully on squared paper turning in the same direction each time by a right angle.
See what you get and colour it in if you like.

You may like to change a rule or two after a while. (For example, you could change the turn to $60^\circ$ instead of $90^\circ$.)

Please send us your pictures.

A very kind teacher Mr Morrison from NSW Australia posted us a Scratch program to use for the same activity you can find it at https://scratch.mit.edu/projects/122888029/