Growing Rectangles
Growing Rectangles printable sheet
Imagine a rectangle with an area of $20$cm$^2$
What could its length and width be? List at least five different combinations.
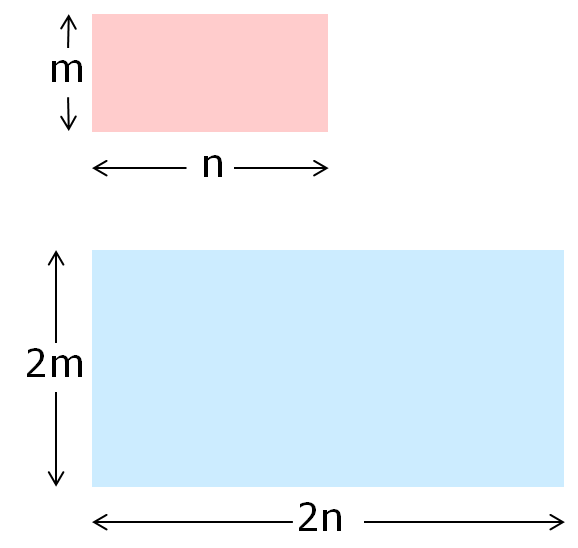
If you enlarge each of your rectangles by a scale factor of 2, what would their new dimensions be?
What would their areas be?
What do you notice?
What happens when you enlarge rectangles with different areas by a scale factor of 2?
What if you enlarge them by a scale factor of 3? Or 4? Or 5 ...? Or $k$?
What if $k$ is a fraction?
Explain and justify any conclusions you come to.
Do your conclusions apply to plane shapes other than rectangles?
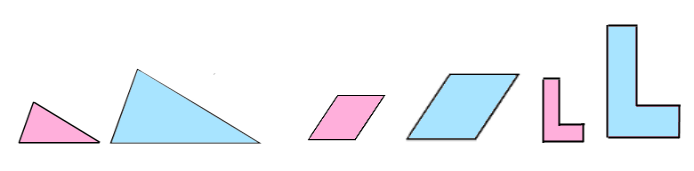
Now explore what happens to the surface area and volume of different cuboids when they are enlarged by different scale factors.
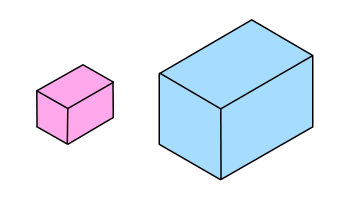
Do your conclusions apply to solids other than cuboids?
This problem is based on an idea suggested by Tabitha Gould.
You may also like
Hex
Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other.
