Transformation Game

Why not challenge a friend to play this transformation game?
 

You will need:

• Board - print this and then enlarge onto A3 paper with a photocopier if you have access to one. Otherwise, you can print it on two sheets of A4 paper and join them together using the bigger version.
   
• Cards - print this sheet three times and cut out the cards to make a pack of 45 transformation cards.
• 
• Counter (you could cut out a triangle to use as a counter)
   
• 2 - 4 players
   

How to play:

• Shuffle the cards, deal five to each player and place the rest of the pack face down on the table. Put the counter on the triangle marked "start".

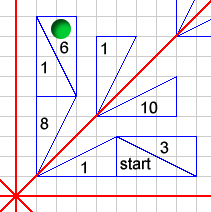• Players take it in turns to move. When it is a player's turn, s/he must try to move the playing piece from where it is on the board to another of the marked triangles. S/he must use a transformation or combination of transformations corresponding to one or more of the cards in his/her hand. In the case of more than one card, the intermediate positions of the playing piece need not correspond to a marked triangle.

• When a player has moved, s/he throws away the card or cards s/he has used, and replaces it (or them) with cards from the unused pile.
   
• The player scores the number of points corresponding to the number on the triangle where s/he finally lands.
   
• If a player cannot move (or does not wish to move), s/he may throw away one card and replace it with another.
   
• When using a joker, a player must announce what it represents before s/he uses it.
   
• If a player makes a mistake, the playing piece is returned to its last position and the player at fault misses that turn.
   
• The game ends when the pile of unused cards is empty and no one can move. The player with the highest total score wins.