Table Patterns Go Wild!

Age 7 to 11

Challenge Level Yellow star

Rajeev from Fair Field Junior looked at the first row of grids in the problem and said:

In any grid where every $4$th square is shaded then it will contain multiples of $4$ and so on. In the $7$ grid as every $3$rd square is shaded it has multiples of $3$, in the $5$ grid where every $2$nd square is shaded you get multiples of $2$ and in the $8$ grid where every $5$th square is shaded you get multiples of $5$ and if you get a negative diagonal line in the $6$ grid starting from the $1$st square in the $2$nd row you get multiples of $7$.

For the row of grids where you could only see the top of them, Rajeev said:

If it's a $7$ grid and every $4$th square is shaded it contains multiples of $4$. I have also noticed that the lines run parallel diagonally and the difference between the shaded squares is $3$ in the $7$ grid so every diagonal line will contain multiples of $4$.

If the lines run diagonally parallel and the difference between shaded squares in a row is $2$ then all the diagonal lines will have multiples of $3$.

Where every $2$nd square is shaded then it contains multiples of $2$ and as explained the last column in any grid will contain multiples of that grid.

Rajeev goes on to say that where the edges are not shown you can still identify the tables:

In the $1$st grid the line is negative running diagonally and if more than $4$ squares are shaded it must be a $6$ grid or more and the tables could be $7$ or more.

What can we say about the relationship between the grid size and times table in this first grid, I wonder?

In the $2$nd grid as the line is positive and running diagonally and at least $4$ squares are shaded the grid must be at least $5$ by $5$ or more.

With the $3$rd pattern it is a $9$ grid and contains $6$ times table, because the difference between the squares horizontally is $5$ and vertically $1$. The grid must be a multiple of $3$.

With the $4$th pattern it is an $8$ grid and has multiples of $3$. The grid could also be $11$, $14$, $17$, $20$, $23$ ... .

The last grid must be $8$ or more.

I wonder what else we can say about the last grid? Fantastic work, Rajeev. You've explained your thinking very clearly.

Grace, Libby, Chloe-Anne and Becky from Maldon Primary School looked at the patterns of tables on differently-sized grids. Chloe-Anne pointed out:

$2$x on an even grid will go down in columns and on an odd grid it is like a checkerboard.

Becky noticed:

If you have a number and it's that type of number grid eg $7$ by $7$ grid means that you would get the $7$ times table going downwards or eg $5$ by $5$ grid you would get the $5$ times table going downwards in a straight line.

So, I think Becky is saying that when you create the pattern of the times table that is the same as the size of the grid, you get a straight line going downwards, or vertically. Well spotted!

Mrs Cresswell's Maths Group from Manor School, Didcot wrote:

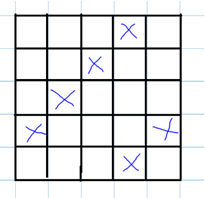
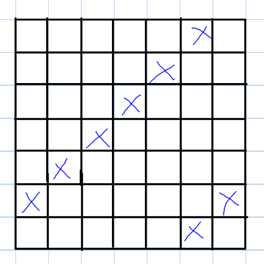
We really enjoyed trying the times tables on $10$x$10$ grids and we found a pattern we could describe for all the times tables except the $7$ times table!
We noticed that the $9$x table had a diagonal pattern because the grid was one larger than $9$, so the number we coloured in ended up one further back on the row below each time.
We tried this out with other numbers that were one less than the size of the grid, and found that this always makes a diagonal pattern. We drew a picture of the $4$x table on a $5$x$5$ grid and the $6$x table on a $7$x$7$ grid to show you:

We wanted to make a diagonal going the other way, so we tried times tables that were one bigger than the grid. We did the $11$x table on a $10$x$10$ grid, and got a diagonal going down from left to right, because the tens and the units got bigger each time.

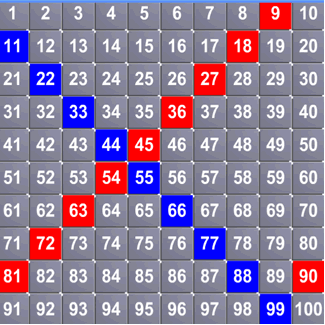
Thank you to everyone who submitted solutions to this problem. There's so much to explore here, isn't there?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Table Patterns Go Wild!

You may also like

Chocolate

Four Triangles Puzzle

Cut it Out