Counting Cogs

This problem has been designed to be worked on in a group. For more details about how you might go about doing this, please read the Teachers' Notes.

Here are nine different cogs:





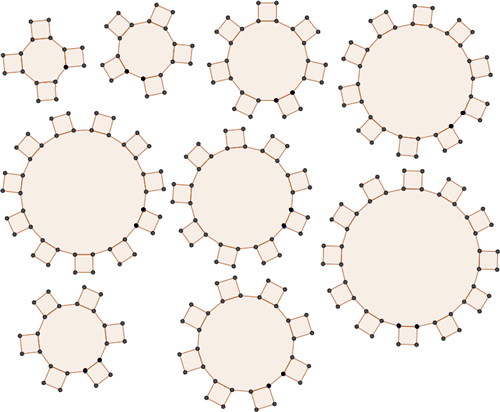
Take a pair of cogs. Mark a tooth on the first cog with a black dot. As the two cogs move around each other, note which gaps on second cog the marked tooth goes in to.

Here are some examples, where the first cog in the pair is one with six teeth.

When the second cog also has six teeth, the marked tooth only ever meets one of the six gaps on the second cog (the one also marked with a black dot):
 

When the second cog has seven teeth, the marked tooth meets each of the different coloured gaps on the second cog:
 

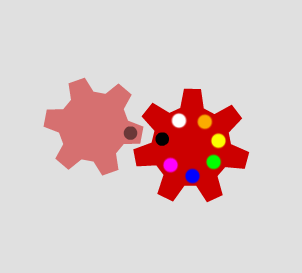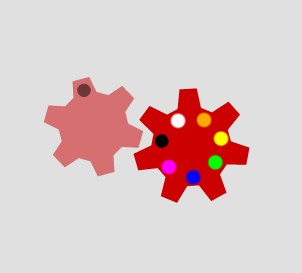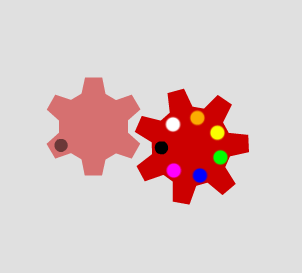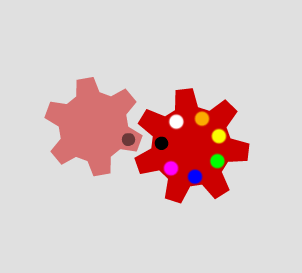
When the second cog has nine teeth, the marked tooth only goes in to the cogs marked with black or yellow dots:
 


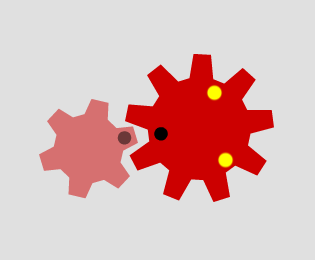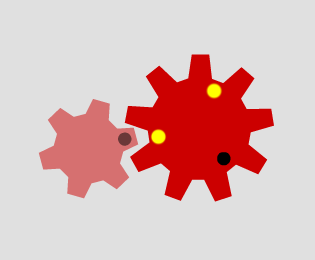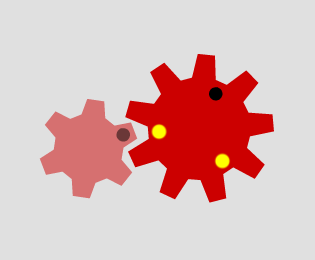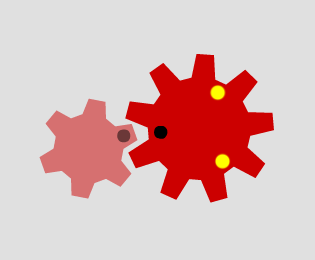
Which pairs of cogs let the coloured tooth go into every 'gap' on the other cog?

Which pairs do not let this happen? Why?

Can you explain how to determine which pairs will work, and why?

You could cut out the cogs from these sheets to try out your ideas.