Skip over navigation
With painting by numbers, a line drawing is split into regions which are to be painted according to the rules that:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider these two images, one made from intersecting ellipses and one made from overlapping rectangles (include the outer square boundaries in the image)
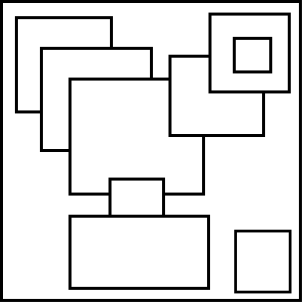
Part 1
What is the smallest number of colours needed to colour these pictures according to the colouring rules? Prove your result clearly.
Consider the more general question of colouring other pictures created from intersecting ellipses or overlapping squares. Can you form any well-considered conjectures, prove any results or find any interesting examples?
Part 2
Imagine that painting by numbers pictures are draw on a sheet of rubber which can be distorted - stretched or shrunk at any point. How many 'topologically different' sorts of pictures would there be with two, three or four regions? How could these be painted according to the rules?
Extension: Try the Torus Patterns problem.
NOTES AND BACKGROUND
The issues raised in this problem concern a famous mathematical theorem the proof of which was surrounded by difficulty and controversy. You can read about this in our fascinating mathematical history article 'The Four Colour Theorem'. The issues raised by the theorem are accessible at school level, but full understanding takes you right up to university level pure mathematics.
Mathematics and art are in many ways closely related. You can read more about the mathematics of art on the Plus website pages
Art + Math = x by Carla Farsi with Marianne Freiberger
Teacher package: Maths and art contains many fascinating links and articles
Painting by Numbers
Age 16 to 18
Challenge Level 
With painting by numbers, a line drawing is split into regions which are to be painted according to the rules that:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider these two images, one made from intersecting ellipses and one made from overlapping rectangles (include the outer square boundaries in the image)
Part 1
What is the smallest number of colours needed to colour these pictures according to the colouring rules? Prove your result clearly.
Consider the more general question of colouring other pictures created from intersecting ellipses or overlapping squares. Can you form any well-considered conjectures, prove any results or find any interesting examples?
Part 2
Imagine that painting by numbers pictures are draw on a sheet of rubber which can be distorted - stretched or shrunk at any point. How many 'topologically different' sorts of pictures would there be with two, three or four regions? How could these be painted according to the rules?
Extension: Try the Torus Patterns problem.
NOTES AND BACKGROUND
The issues raised in this problem concern a famous mathematical theorem the proof of which was surrounded by difficulty and controversy. You can read about this in our fascinating mathematical history article 'The Four Colour Theorem'. The issues raised by the theorem are accessible at school level, but full understanding takes you right up to university level pure mathematics.
Mathematics and art are in many ways closely related. You can read more about the mathematics of art on the Plus website pages
Art + Math = x by Carla Farsi with Marianne Freiberger
Teacher package: Maths and art contains many fascinating links and articles
You may also like
Where Do We Get Our Feet Wet?
Professor Korner has generously supported school mathematics for more than 30 years and has been a good friend to NRICH since it started.
Links and Knots
Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots, prime knots, crossing numbers and knot arithmetic.
Earth Shapes
What if the Earth's shape was a cube or a cone or a pyramid or a saddle ... See some curious worlds here.