Skip over navigation
To get started, simply try colouring in some pictures. This is the best way to get a feel for the structure of the problem.
Once you have made a conjecture, you will be able to test it out on other pictures to gain confidence in its validity, or to reject it if you create a counter example.
To prove a conjecture ask yourself the question: what could go wrong to make it false? This is a good way to focus on the key underlying mathematical structure.
To begin with, you can certainly pick a region and give it a colour. The colour of certain other regions will necessarily follow. Try this approach and see where you and up with a choice.
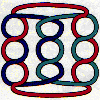
For the question of toplogy, ask yourself why the first of these two images are topologically the same whereas the second pair are not:
Painting by Numbers
Age 16 to 18
Challenge Level 
To get started, simply try colouring in some pictures. This is the best way to get a feel for the structure of the problem.
Once you have made a conjecture, you will be able to test it out on other pictures to gain confidence in its validity, or to reject it if you create a counter example.
To prove a conjecture ask yourself the question: what could go wrong to make it false? This is a good way to focus on the key underlying mathematical structure.
To begin with, you can certainly pick a region and give it a colour. The colour of certain other regions will necessarily follow. Try this approach and see where you and up with a choice.
For the question of toplogy, ask yourself why the first of these two images are topologically the same whereas the second pair are not:
You may also like
Where Do We Get Our Feet Wet?
Professor Korner has generously supported school mathematics for more than 30 years and has been a good friend to NRICH since it started.
Links and Knots
Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots, prime knots, crossing numbers and knot arithmetic.
Earth Shapes
What if the Earth's shape was a cube or a cone or a pyramid or a saddle ... See some curious worlds here.