Skip over navigation
In minimalist, abstract or computer generated art a real object is often represented by a simplified set of shapes and curves.
For example, this image of the famous artist Mondrian might be transformed or represented by transformations of standard mathematical functions as follows:
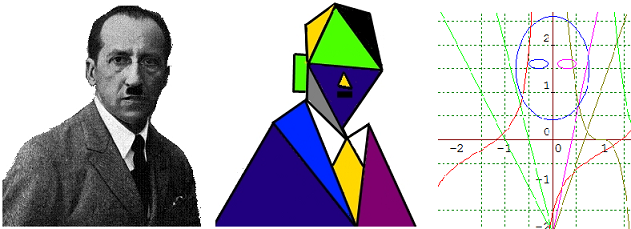
Consider some objects and works of art. Think how they might be broken down into shapes or segments of lines and curves. How many such shapes or line and curve segments would be needed to give a recognisable abstract impression of the pictures? Imagine how you could encode your lines and curves mathematically by imposing a coordinate grid on the picture.
Use a graphing software package to create your impressions mathematically. Your toolkit contains the standard mathematical functions: Polynomials, sin, cosh, sinh and also the techniques of composition and transformation of functions.
You might want to print off the picture, highlight the segments of the curves of interest and colour according to the colouring schemes in Painting by Numbers.
Please send us any of your creations!
If you want to focus on pictures made with straight lines, see the problem Painting Between The Lines.
NOTES AND BACKGROUND
The mathematical issues raised in this problem are directly related to the creation of computer generated art where images are typically encoded mathematically; indeed if you zoom in closely to any digital image you will see that it is encoded as squares or blocks of uniform colours which give the impression of an analogue image.
In computer gaming, images are first represented minimally and digitally using mathematics; the next phase is to animate the images.
You can read more about the mathematics of art on the Plus website pages
Digital Art by Lewis Dartnell
Teacher package: Maths and art contains many fascinating links and articles
Painting by Functions
Age 16 to 18
Challenge Level 
In minimalist, abstract or computer generated art a real object is often represented by a simplified set of shapes and curves.
For example, this image of the famous artist Mondrian might be transformed or represented by transformations of standard mathematical functions as follows:
Consider some objects and works of art. Think how they might be broken down into shapes or segments of lines and curves. How many such shapes or line and curve segments would be needed to give a recognisable abstract impression of the pictures? Imagine how you could encode your lines and curves mathematically by imposing a coordinate grid on the picture.
Use a graphing software package to create your impressions mathematically. Your toolkit contains the standard mathematical functions: Polynomials, sin, cosh, sinh and also the techniques of composition and transformation of functions.
You might want to print off the picture, highlight the segments of the curves of interest and colour according to the colouring schemes in Painting by Numbers.
Please send us any of your creations!
If you want to focus on pictures made with straight lines, see the problem Painting Between The Lines.
NOTES AND BACKGROUND
The mathematical issues raised in this problem are directly related to the creation of computer generated art where images are typically encoded mathematically; indeed if you zoom in closely to any digital image you will see that it is encoded as squares or blocks of uniform colours which give the impression of an analogue image.
In computer gaming, images are first represented minimally and digitally using mathematics; the next phase is to animate the images.
You can read more about the mathematics of art on the Plus website pages
Digital Art by Lewis Dartnell
Teacher package: Maths and art contains many fascinating links and articles
You may also like
Vector Walk
Starting with two basic vector steps, which destinations can you reach on a vector walk?
Sheep in Wolf's Clothing
Can you work out what simple structures have been dressed up in these advanced mathematical representations?
Vector Journeys
Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?