Vector Journeys

Vector Journeys printable sheet

Charlie likes to go for walks around a square park.
Here is a diagram of the journey he took one day:

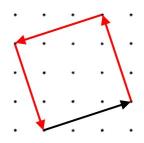
He started his journey by walking along the black vector $\pmatrix{3\cr 1}$
What vectors did he need to walk along to complete his journey?
 
Draw some other square parks that Charlie could walk around, and find the vectors that would describe his journey.
 
Can you describe and explain any relationships between the vectors that determine Charlie's journey around any square park?

Once you know the first vector of a journey, can you work out what the second, third and fourth vectors will be? Is there more than one possibility?
 
 
Alison likes to walk across parks diagonally.
One day, she walked along the blue vector $\pmatrix{2\cr 4}$:

 

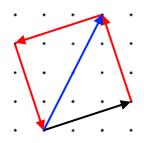
• Can you describe any relationships between the vectors that determine Alison's and Charlie's journey, for any square park?
   
• Given the vector that describes Alison's journey, how can you work out the first stage of Charlie's journey?
   
• If all square parks have their vertices on points of a dotty grid, what can you say about the vectors that describe Alison's diagonal journey?

Can you explain and justify your findings?