Light the Lights Again

We had lots of excellent solutions submitted for this problem, so thank you to everybody who sent in their ideas.

Ishaan from Chigwell School in the UK worked out the rules for each colour:

Rules:
Green: Even number
Red: Number ending in 1 or 6 - The final answer will end in 6, because otherwise it will not be an even number which is needed for green.
Blue: Adding next increment of odd number to the previous number starting from 0. So, 0, 1, 4, 9, 16, 25, 36, 49, 64
Yellow: Adding to the previous number, increasing by 1 each time. So, 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55

Answer: 36

Thank you for sending us your ideas, Ishaan - I particularly like how you realised that the number that turns on all the lights must end in a 6. Ishaan has described the sequence 1, 4, 9, 16, 25, etc. as adding the next odd number each time, which is a very interesting way of thinking about it. 

Michelle from Westridge School in the USA noticed the same pattern, and she explained her thinking:

Blue light: When I put each of the numbers 0, 1, 4, 9, and 16 (etc.) in the machine, the blue light shone. I found that the difference between the previous number and the following number, was the next larger odd number. For example, the difference of 0 to 1, is one. 1 to 4, is three. 4 to 9, is five. The difference changes and is the next odd number. The answers are also all square numbers.

Well done, Michelle! I wonder why the sequence of square numbers goes up by an increasing odd number each time?

Michelle also sent us a photo and explained how she found the smallest number that lights up all the lights:

Finally, I wrote down all the numbers until the twentieth number in each of the patterns. I chose to write 20 numbers because the common number for each pattern might not appear in the beginning. I followed each rule one by one until I got four long lists of 20 numbers each. I compared each line to try to find one number that all the lists had. In order to find the smallest, I looked closest to the beginning of the lists where the numbers were the smallest. At the end, the smallest common number I found was 36.

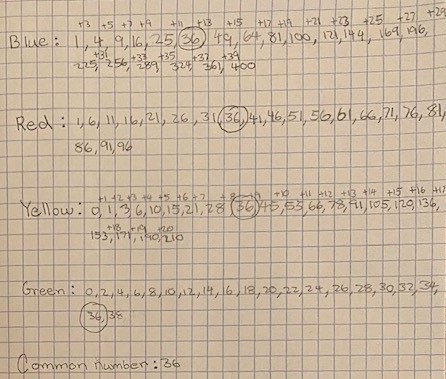
Tushar from NPS Rajajinagar in India looked at the numbers from 1-20 to work out what the patterns were:

I started by making a table with rows indicating the numbers starting from 1 and columns indicating Red, Yellow, Green and Blue colours. I starting putting the numbers from 1 to 20 one after another into the box and marked the results on my table by putting 'x'.

By the time I reached 10, it was clear that Green glowed for all even numbers.

By the time I reached 16, it was clear that Red glowed when I typed a number that was multiple of 5 plus 1, example, 15+1=16.

Yellow was tricky, but by the time I reached 28, I saw that the gap between the numbers for which Yellow glowed increased by 1 starting with number 1.

Blue was the trickiest, I could only figure out the pattern by 25 that the gap between the numbers for which blue glowed increased by 2 starting from number 1.

Then, by the above patterns, 36 was the first number which made all lights glow.

Well done, Tushar - I found it interesting to see at what point you spotted each pattern! Take a look at Tushar's table to see how he chose to record the different lights that came on for each number.

The children from Fordham All Saints Church of England Primary School described the method they used:

Firstly, we drew a table. This displayed the colours from the interactive board we used (red, yellow, green and blue). We noted down the numbers which lit each light. We also had a column in our table for numbers which didn't light any lights.

Green:
This was the first colour we found the answer to. It was the easiest and certainly the most obvious. Green was proven to be all even numbers.

Red:
Next, we worked out red. Our first hypothesis for this was that all the numbers had 6 and 1 in them. But that wasn't quite right. 4.6 did not light it up. We then realised that all numbers ending in 1 and 6 are 1 more than multiples of 5.

Blue:
Our first hypothesis for blue was that the numbers were all in the four times table, but 25 disproved this. We then realised that they were all in fact square numbers. 

Yellow:
This was the most difficult one to work out, we struggled to even make a hypothesis. However, we were encouraged to attempt to draw the numbers as shapes and one of us realised that all of the numbers made pyramids. These numbers are known as triangular numbers. 

Green = even numbers
Red = numbers 1 more than multiples of 5
Blue = square numbers
Yellow = triangular numbers 

We also discovered that 36 is the lowest number possible to light all of the lights.

Well done to all of you! I enjoyed reading about your hypotheses at the different stages of your investigation. 

James from Hamstel Junior School in England explained how he found the number that turned on all the lights, once he'd worked out the rules:

Once I knew the four rules, I had to find a square number that ended in 6 and check that it was also a triangle number which meant that the answer was 36.

Good idea, James. I wonder if we could use this method to find bigger numbers that would turn on all of the lights...

Some children from The British School of Paris in France looked at what happens when you enter different types of numbers into the box. Agniia noticed:

Some negative numbers work, but only if the number fits into one of the rules.

This is interesting, Agniia. I wonder which lights can come on when you type negative numbers into the box. 

Sara and Kate from University of Chicago Laboratory Schools in the USA sent us some clear explanations of each rule. They chose to write the nth triangle number as the sum of the numbers from 1 to n. It looks like there are lots of different ways to write the rule for the yellow light!

Lots of other children also sent in very good explanations of these patterns. Thank you to: all the children at Aberfoyle Primary School in Scotland; Vir and Anya from Nord Anglia International School in Dubai; Harvey from St Nicholas School in the UK; Nithya from Thompson Elementary in the United States; Jayden from BVIS in Vietnam; Lydia from Lindfield Primary Academy in the UK; Charlotte from Mundford Primary in the UK; Noah from Gaelscoil Riada in Ireland; Sue-Anne from Garden International School in Malaysia; Sarina and Sabrina from University of Chicago Lab School in the USA; all the children in the Maths Challenge Club at King Henry VIII Preparatory School in the UK; Milly, Alice and Janvi from St Peter's C of E Primary School in England; and Ethan, Eric and Josh from St Charles Ryde Primary School in Australia.