Skip over navigation
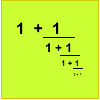

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Quad Solve
Age 16 to 18
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
Find all real solutions to this equation:
$$\left(2-x^2\right)^{x^2-3\sqrt{2}x+4} = 1$$
Extension: What if $x$ is permitted to be a complex number?
Did you know ... ?
Quadratic equations and powers are commonly used throughout school and university mathematics and beyond. It is also important to remember that algebraic manipulations might not necessarily find all solutions to a problem; you always need to reason carefully that all possibilities have been considered. Moreover, in complicated situations it is necessary to check that all proposed solutions unearthed by algebra are in fact valid solutions. Powers, roots and quadratics all link together very nicely when complex numbers are considered.
Quadratic equations and powers are commonly used throughout school and university mathematics and beyond. It is also important to remember that algebraic manipulations might not necessarily find all solutions to a problem; you always need to reason carefully that all possibilities have been considered. Moreover, in complicated situations it is necessary to check that all proposed solutions unearthed by algebra are in fact valid solutions. Powers, roots and quadratics all link together very nicely when complex numbers are considered.
You may also like
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Target Six
Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.

