Skip over navigation
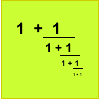

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Quad Solve
Age 16 to 18
ShortChallenge Level 





To do this problem you will need to know that $a^0 = 1$ when $a\neq
0$ and $1^b=1$ for any $b$ along with other power manipulations
which are needed from the beginning of C1.
Note that $0^0$ is not defined as a number.
You will also need to know the formula for the solution of a quadratic equation.
If you are studying complex numbers then you can also bring those ideas into the problem if desired.
Note that $0^0$ is not defined as a number.
You will also need to know the formula for the solution of a quadratic equation.
If you are studying complex numbers then you can also bring those ideas into the problem if desired.
You may also like
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Target Six
Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.

