The Sign of the Times

Consider curves that pass through the origin and have the required property that  $$f(x)\times\frac{df(x)}{dx} \leq 0$$
Suppose $f(x)$ is positive for some positive $x=x_0$. If we require $f(0)=0$,  this means the gradient must be positive for part of the interval $[0, x_0]$, which would mean that $f(x)\times\frac{df(x)}{dx} > 0$ for these points.

Similarly, if we suppose $f(x)$ is negative for some positive $x=x_0$, we find that the gradient will have to be negative for part of the interval $[0,x_0]$, which would mean that $f(x)\times\frac{df(x)}{dx} > 0$ for these points.

We therefore need $f(x)\equiv0$ for all $x\ge0$.

For $x< 0$, we can choose f so that $f(x)\not\equiv0$. For example, we can choose f to be positive but have a negative gradient for all $x< 0$, which would mean $f(x)\times\frac{df(x)}{dx} < 0$.

Let's try choosing $f=-x$ for $x< 0$:

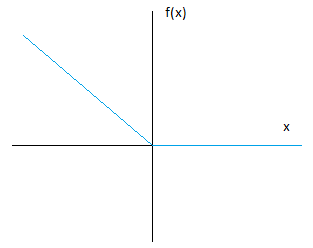
This satisfies the condition $f(x)\times\frac{df(x)}{dx} \leq 0$ for all x. The other condition was that the derivative exists for all x. For $x> 0$, $\frac{df(x)}{dx} = 0$, and for $x< 0$, $\frac{df(x)}{dx}=1$. However, what's the derivative at $x=0$? As we approach from the right, $\frac{df(x)}{dx}=1$, but as we approach from the left, $\frac{df(x)}{dx}=0$. Therefore, our derivative doesn't exist at $x=0$ as was required, so we need to think of something else! (For a rigorous treatment of this, see a first year analysis course.)

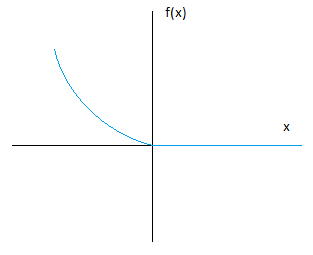
We need to think of another function with behaviour like the previous one, but with a gradient of $0$ as we approach $x=0$. Let's try the next simplest polynomial, a quadratic: $f(x)  = x^2$. This passes through the origin, and has derivative $\frac{df(x)}{dx}=2x$. So at $x=0$, the derivative is $0$ as we approach from both directions, so therefore exists. We've found a function that has the desired properties!

If we don't have the requirement that $f(0)=0$, there are lots of examples, e.g. $f(x)=exp(-x)$.  

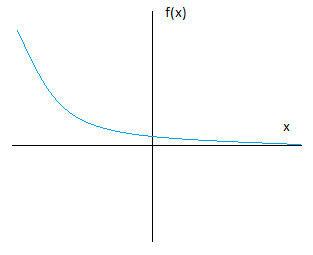
Here, $f(x)>0$ for all x, and the gradient exists for all x and is negative: $\frac{df(x)}{dx} = -exp(-x) <0,$ as required.