Skip over navigation
Forming an equation using the amounts added and subtracted
To shift the sequence along $D$ spaces,
from $(1111)+ (1112)+( 1113)+, \dots, (1111 + N-1)$
to $(1111+D)+(1112+D) + (1113+D) + \dots+(1111 + N -1+ D),$
you add $D$ to each term, so you add it $N$ times, since there are $N$ terms.
That is the same as adding a total of $N\times D$.
Then removing the first term, $1111+D$, takes the sum back to its original value.
So $N\times D$ must be equal to $1111+D$.
$$\begin{align}ND&=1111+D\\\Rightarrow ND-D&=1111\\\Rightarrow (N-1)D&=1111\end{align}$$
$N$ and $D$ are both integers, so $N-1$ and $D$ must be factors of $1111$.
$1111=11\times101$, which are both prime, so all of the possible values of $N$ and $D$ are shown below:
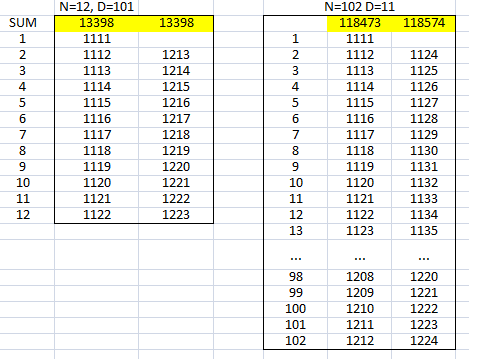
You can see some of these sums in action on the spreadsheet screenshot at the bottom of the page.
Using the formula for the sum of the first $n$ natural numbers
The sum of the first $n$ natural numbers is equal to $$
1+2+\dots + (n-1) + n =\frac{1}{2}n(n+1)
$$
Its easier in a problem like this to introduce some notation. Let's write $S(n)$ to mean the sum of the first $n$ natural numbers.
Since the two sums are equal we have
$$
S(1111+N-1)-S(1110) = S(1111+N -1 +D) - S(1111 + D)
$$
Let's put the formula into each of these and cancel each factor of a half.
$$
(1110+N)(1111+N)-(1110)(1111)=(1110+N+D)(1111+N+D)-(1111+D)(1112+D)
$$
Before leaping in we can see that many parts cancel, so we can put
$$
2221N + N^2 = 2221(N+D) + (N+D)^2 - 2223D - D^2- 2222
$$
Collecting things together gives
$$
D(N-1) = 1111
$$
Now for a bit of number theory: $1111 = 11\times 101$, or $1\times1111$. Thus, for solutions we require:
$D = 11, N=102$ or $D=101, N=12$ or $D=1,N=1112$ or $D=1111,N=2$.
You can see some of these sums in action on this spreadsheet screenshot


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
AP Train
Age 16 to 18
ShortChallenge Level 





- Problem
- Solutions
Forming an equation using the amounts added and subtracted
To shift the sequence along $D$ spaces,
from $(1111)+ (1112)+( 1113)+, \dots, (1111 + N-1)$
to $(1111+D)+(1112+D) + (1113+D) + \dots+(1111 + N -1+ D),$
you add $D$ to each term, so you add it $N$ times, since there are $N$ terms.
That is the same as adding a total of $N\times D$.
Then removing the first term, $1111+D$, takes the sum back to its original value.
So $N\times D$ must be equal to $1111+D$.
$$\begin{align}ND&=1111+D\\\Rightarrow ND-D&=1111\\\Rightarrow (N-1)D&=1111\end{align}$$
$N$ and $D$ are both integers, so $N-1$ and $D$ must be factors of $1111$.
$1111=11\times101$, which are both prime, so all of the possible values of $N$ and $D$ are shown below:
| Product $(N-1)\times D =1111$ | $N$ and $D$ |
|---|---|
| $1111\times1$ | $N=1112,D=1$ |
| $1\times1111$ | $N=2,D=1111$ |
| $11\times101$ | $N=12,D=101$ |
| $101\times11$ | $N=102,D=11$ |
You can see some of these sums in action on the spreadsheet screenshot at the bottom of the page.
Using the formula for the sum of the first $n$ natural numbers
The sum of the first $n$ natural numbers is equal to $$
1+2+\dots + (n-1) + n =\frac{1}{2}n(n+1)
$$
Its easier in a problem like this to introduce some notation. Let's write $S(n)$ to mean the sum of the first $n$ natural numbers.
Since the two sums are equal we have
$$
S(1111+N-1)-S(1110) = S(1111+N -1 +D) - S(1111 + D)
$$
Let's put the formula into each of these and cancel each factor of a half.
$$
(1110+N)(1111+N)-(1110)(1111)=(1110+N+D)(1111+N+D)-(1111+D)(1112+D)
$$
Before leaping in we can see that many parts cancel, so we can put
$$
2221N + N^2 = 2221(N+D) + (N+D)^2 - 2223D - D^2- 2222
$$
Collecting things together gives
$$
D(N-1) = 1111
$$
Now for a bit of number theory: $1111 = 11\times 101$, or $1\times1111$. Thus, for solutions we require:
$D = 11, N=102$ or $D=101, N=12$ or $D=1,N=1112$ or $D=1111,N=2$.
You can see some of these sums in action on this spreadsheet screenshot

You may also like
Circles Ad Infinitum
A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
Climbing Powers
$2\wedge 3\wedge 4$ could be $(2^3)^4$ or $2^{(3^4)}$. Does it make any difference? For both definitions, which is bigger: $r\wedge r\wedge r\wedge r\dots$ where the powers of $r$ go on for ever, or $(r^r)^r$, where $r$ is $\sqrt{2}$?

