Skip over navigation

Sitting Round the Party Tables

Age 5 to 11

Challenge Level Yellow star

Primary curriculum

Sitting Round the Party Tables

So, you are at the party and sitting around the table with seven friends.

At the top left-hand corner is the friend who is giving the party. S/he has a bag of sweets and starts giving them out in a clockwise direction: one for her/himself, two for the next person and three for the next and so on.

There are other similar parties going on at the same time. They have bigger square tables with more children sitting round on each side.

Explore and compare all the tables: 2 on each side, 3 on each side, 4 on each side and $5$ on each side.

You could look at:

the total number of sweets that children sitting opposite each other have;

the total number of sweets needed for each size of table;

the total number of sweets belonging to children who are diagonally opposite.

Then, what about five- and six-sided tables?

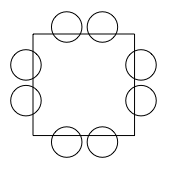
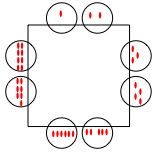
Why do this problem?

This activity gives pupils the opportunity to explore some simple number relationships, from which they can be encouraged to make some generalisations. It may also be a good context in which to help pupils ask their own questions - "I wonder what would happen if we ...?" showing their curiosity. You will be aware that a lot of perseverance is helpful in solving this challenge. The "Teacher Support" at the bottom of this page is recommended in regard to the curiosity aspect of this task.

Possible approach

With younger pupils or those with little experience of exploration in mathematics and talking about their mathematical thoughts, it would be good to act out the problem as first described.

With more experienced pupils you could just present the challenge orally and ask them to explore further. Encourage learners to write down all the things they notice. It might also be appropriate for you to bring everyone together after some time to discuss how they are recording their work.

Invite pupils to ask and begin to answer their own questions: "I wonder what would happen if I ...?". You could use some of the suggestions in the problem itself to prompt those who may not be used to doing this.

Key questions

Tell me about what you have noticed about the numbers of sweets.

What else are you going to explore?

Tell me about what's going on at the other party tables.

Are there any special things you notice about the seats in particular places?

Possible extension

Some pupils might look at generalisations that they can say about tables of ANY size or of ANY shape.

Possible support

Some pupils may find it helpful to approach the problem using practical equipment, for example using counters to represent the sweets and having 'tables' made out of paper or card.

Teacher Support

This task was created to help in the pursuance of curiosity within the Mathematics lessons.
Help may be found in the realm of curiosity in watching parts of these excellent videos.
Firstly "The Rise & Fall of Curiosity", particularly the extract [23.50 - 37.15] on "adult encouragement answering and teacher behaviour."
Secondly, "The Hungry Mind: The Origins of Curiosity", particularly the extract [8.22 - 12.29] on "Children asking questions.

First can also be found at - https://www.youtube.com/watch?v=X-0NOrIU67w
Second can also be found at https://www.youtube.com/watch?v=Wh4WAdw-oq8

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Sitting Round the Party Tables

Sitting Round the Party Tables

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

Teacher Support

You may also like

I'm Eight

Let's Investigate Triangles

Noah